题目内容
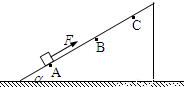
如图所示，一光滑斜面固定在水平地面上，质量m=1kg的物体在平行于斜面向上的恒力F作用下，从A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达C点时速度为零．每隔0.2s通过传感器测得物体的瞬时速度，下表给出了部分测量数据．| t/s | 0.0 | 0.2 | 0.4 | … | 2.2 | 2.4 | … |
| v/m?s-1 | 0.0 | 1.0 | 2.0 | … | 3.3 | 2.1 | … |
【答案】分析：（1）先由匀变速运动求出加速度的大小，再由受力分析和牛顿第二定律求出力的大小；
（2）利用匀变速直线运动中速度与时间的关系求出F作用的时间．
解答：解：（1）加速阶段由加速度的定义知，加速度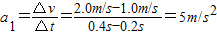
减速阶段加速度大小为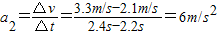
加速阶段中由牛顿第二定律得：F-mgsinθ=ma1
减速阶段中由牛顿第二定律得：mgsinθ=ma2
由上两式代入数据得：F=m（a1+a2）=11N
（2）撤力瞬间速度最大a1t=v+a2（t'-t）（其中：v=3.3m/st'=2.2s）
解得t=1.5s
答：（1）恒力的大小为11N
（2）撤去外力F的时刻为1.5s末
点评：本题考查匀变速直线运动规律，是典型的牛顿定律解题中的一类．关键是应用加速度定义和牛顿第二定律表示加速度的大小，这是一道好题．
（2）利用匀变速直线运动中速度与时间的关系求出F作用的时间．
解答：解：（1）加速阶段由加速度的定义知，加速度
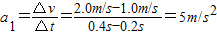
减速阶段加速度大小为
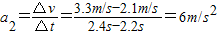
加速阶段中由牛顿第二定律得：F-mgsinθ=ma1
减速阶段中由牛顿第二定律得：mgsinθ=ma2
由上两式代入数据得：F=m（a1+a2）=11N
（2）撤力瞬间速度最大a1t=v+a2（t'-t）（其中：v=3.3m/st'=2.2s）
解得t=1.5s
答：（1）恒力的大小为11N
（2）撤去外力F的时刻为1.5s末
点评：本题考查匀变速直线运动规律，是典型的牛顿定律解题中的一类．关键是应用加速度定义和牛顿第二定律表示加速度的大小，这是一道好题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
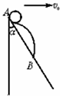如图所示，一光滑斜面与竖直方向成α角，一小球有两种方式释放：第一种方式是在A点以速度v0平抛落至B点；第二种方式是在A点松手后沿斜面自由滑下，?
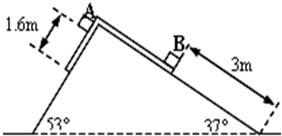如图所示，一光滑斜面固定在水平面上，斜面上放置一质量不计的柔软薄纸带．现将质量为M=2kg的A物体和质量m=1kg的B物体轻放在纸带上．两物体可视为质点，物体初始位置数据如图，A、B与纸带间的动摩擦因数分别为μA=0.5、μB=0.8（sin37°=0.6，cos37°=0.8，g取10m/s2）．则（ ）
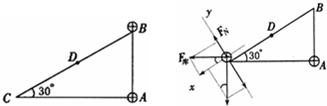如图所示，一光滑斜面的直角点A处固定一带电量为+q，质量为m的绝缘小球，另一同样小球置于斜面顶点B处，已知斜面长为L，现把上部小球从B点从静止自由释放，球能沿斜面从B点运动到斜面底端C处，
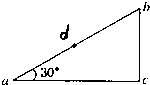如图所示，一光滑斜面的倾角为30°斜边，长为L，其直角点c处固定一带电荷量为+q的绝缘小球，另一电荷量也为+q；质量为m的绝缘小球从b点由静止释放．球能沿斜面从b点运动到a点，d为bc中点，则（ ）
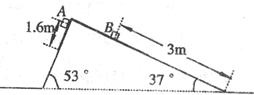（2010?青岛三模）如图所示，一光滑斜面固定在水平面上，斜面上放置一质量不计的柔软薄纸带．现将质量为mA的物体A和质量mB的物体B轻放在纸带上．两物体可视为质点，物体初始位置数据如图所示，A到纸带末端的距离为而x1=l.6m，B放在纸带上距离底端x2=3m．