题目内容
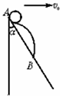如图所示，一光滑斜面与竖直方向成α角，一小球有两种方式释放：第一种方式是在A点以速度v0平抛落至B点；第二种方式是在A点松手后沿斜面自由滑下，?（1）AB的长度
2
| ||
| gsin2α |
2
| ||
| gsin2α |
（2）两种方式到B点，平抛的运动时间为t1，下滑的时间为t2，t1/t2等于
cosα
cosα
?．分析：（1）第一次做的是平抛运动，根据平抛运动的规律，可以求得AB的长度；
（2）从A点下滑的时候，做的是匀加速直线运动，根据牛顿第二定律求出加速度，再根据位移公式可以计算运动的时间，再求它们时间的比值即可．
（2）从A点下滑的时候，做的是匀加速直线运动，根据牛顿第二定律求出加速度，再根据位移公式可以计算运动的时间，再求它们时间的比值即可．
解答：解：两种情况下从A到B只有位移相同，设AB长为L，
（1）根据平抛运动的规律，
水平方向上 Lsinα=v0t1，
竖直方向上 Lcosα=
gt12，
解得 t1=
，
L=
，
即AB的长度为
，
代入上式得 t1=
．
（2）下滑时物体的加速度为a=gcosα，
下滑的位移L=
at22，
解得 t2=
=
，
所以
=cosα．
故答案为：（1）
，（2）cosα．
（1）根据平抛运动的规律，
水平方向上 Lsinα=v0t1，
竖直方向上 Lcosα=
| 1 |
| 2 |
解得 t1=
| Lsinα |
| v0 |
L=
2
| ||
| gsin2α |
即AB的长度为
2
| ||
| gsin2α |
代入上式得 t1=
| 2v0 |
| gtanα |
（2）下滑时物体的加速度为a=gcosα，
下滑的位移L=
| 1 |
| 2 |
解得 t2=
|
| 2v0 |
| gsinα |
所以
| t1 |
| t2 |
故答案为：（1）
2
| ||
| gsin2α |
点评：本题是平抛运动和匀加速直线运动的对比，根据平抛运动和匀加速直线运动的规律分别计算即可，难度不大．
练习册系列答案
一线名师提优试卷系列答案
相关题目
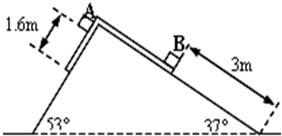如图所示，一光滑斜面固定在水平面上，斜面上放置一质量不计的柔软薄纸带．现将质量为M=2kg的A物体和质量m=1kg的B物体轻放在纸带上．两物体可视为质点，物体初始位置数据如图，A、B与纸带间的动摩擦因数分别为μA=0.5、μB=0.8（sin37°=0.6，cos37°=0.8，g取10m/s2）．则（ ）
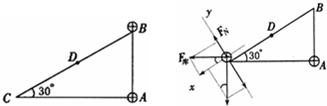如图所示，一光滑斜面的直角点A处固定一带电量为+q，质量为m的绝缘小球，另一同样小球置于斜面顶点B处，已知斜面长为L，现把上部小球从B点从静止自由释放，球能沿斜面从B点运动到斜面底端C处，
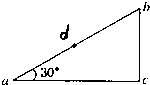如图所示，一光滑斜面的倾角为30°斜边，长为L，其直角点c处固定一带电荷量为+q的绝缘小球，另一电荷量也为+q；质量为m的绝缘小球从b点由静止释放．球能沿斜面从b点运动到a点，d为bc中点，则（ ）
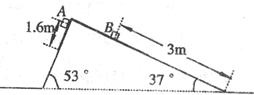（2010?青岛三模）如图所示，一光滑斜面固定在水平面上，斜面上放置一质量不计的柔软薄纸带．现将质量为mA的物体A和质量mB的物体B轻放在纸带上．两物体可视为质点，物体初始位置数据如图所示，A到纸带末端的距离为而x1=l.6m，B放在纸带上距离底端x2=3m．