题目内容
（2010?济南一模）如图所示，光滑圆弧轨道与光滑斜面在B点平滑连接，圆弧半径为R=0.4m，一半径很小、质量为m=0.2kg的小球从光滑斜面上A点由静止释放，恰好能通过圆弧轨道最高点D，g取10m/s2．求：（1）小球最初离最低点C的高度h；
（2）小球运动到C点时对轨道的压力大小FN．
分析：（1）小球恰好能通过圆弧轨道最高点D，说明此时恰好是物体的重力作为向心力，由向心力的公式可以求得在D点的速度大小，从A到D的过程中，物体的机械能守恒，从而可以求得小球释放时离最低点的高度．
（2）在C点时，对物体受力分析，重力和支持力的合力作为向心力，由向心力的公式可以求得小球受得支持力的大小，再由牛顿第三定律可以知道对轨道压力的大小．
（2）在C点时，对物体受力分析，重力和支持力的合力作为向心力，由向心力的公式可以求得小球受得支持力的大小，再由牛顿第三定律可以知道对轨道压力的大小．
解答：解：（1）在D点，速度为vD，则有mg=m
∴vD=2m/s
由A运动到D点，机械能守恒得：
mg(h-2R)=m
∴h=1m
（2）由A运动到C点，机械能守恒mgh=
mvC2
在C点，由向心力公式，得FN-mg=m
∴FN=12N
由牛顿第三定律得压力为12N
答：（1）小球最初离最低点C的高度为1m；
（2）小球运动到C点时对轨道的压力大小为12N．
| vD2 |
| R |
∴vD=2m/s
由A运动到D点，机械能守恒得：
mg(h-2R)=m
| vD2 |
| R |
∴h=1m
（2）由A运动到C点，机械能守恒mgh=
| 1 |
| 2 |
在C点，由向心力公式，得FN-mg=m
| vC2 |
| R |
∴FN=12N
由牛顿第三定律得压力为12N
答：（1）小球最初离最低点C的高度为1m；
（2）小球运动到C点时对轨道的压力大小为12N．
点评：小球的运动过程可以分为三部分，第一段是匀加速直线运动，第二段的机械能守恒，第三段是平抛运动，分析清楚各部分的运动特点，采用相应的规律求解即可．
练习册系列答案
相关题目
（2010?济南一模）老师做了一个物理小实验让学生观察：一轻质横杆两侧各固定一金属环，横杆克绕中心点自由转动，老师拿一条形磁铁插向其中一个小环，后又取出插向另一个小环，同学们看到的现象是（ ）
（2010?济南一模）如图所示，物块A、B叠放在水平桌面上，装砂的小桶C通过细线牵引A、B一起在水平桌面上向右加速运动，设A、B间的摩擦力为f1，B与桌面间的摩擦力为f2，若增大C桶内砂的质量，而A、B仍一起向右运动，则摩擦力f1和f2的变化情况是（ ）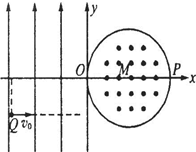
（2010?济南一模）如图所示，在平面坐标系xOy内，第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场，第Ⅰ、Ⅳ象限内存在半径为L的圆形匀强磁场，磁场圆心在M（L，0）点，磁场方向垂直于坐标平面向外．一带正电粒子从第Ⅲ象限中的Q（-2L，-L）点以速度v0沿x轴正方向射出，恰好从坐标原点O进入磁场，从P（2L，0）点射出磁场．不计粒子重力，求：
（2010?济南一模）质量分别为m和2m的物块、B用轻弹簧相连，设两物块与接触面间的动摩擦因数都相同．当用水平力F作用于B上且两物块在粗糙的水平面上，共同向右加速运动时，弹簧的伸长量为x1，如图甲所示；当用同样大小的力F竖直共同加速提升两物块时，弹簧的伸长量为x2，如图乙所示；当用同样大小的力F沿固定斜面向上拉两物块使之共同加速运动时，弹簧的伸长量为x3，如图丙所示，则x1：x2：x3等于（ ）
（2010?济南一模）如图，竖直放置的斜面CD的下端与光滑圆弧轨道ABC的C端相切，圆弧半径为R，圆心与A、D在同一水平面上，∠COB=45°，现将一个质量为m的小物块从A点上方距A竖直高度为h=0.5R的位置无初速释放，小物块从A点进入轨道运动至斜面上D点后返回．