Question

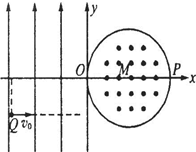（2010?济南一模）如图所示，在平面坐标系xOy内，第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场，第Ⅰ、Ⅳ象限内存在半径为L的圆形匀强磁场，磁场圆心在M（L，0）点，磁场方向垂直于坐标平面向外．一带正电粒子从第Ⅲ象限中的Q（-2L，-L）点以速度v₀沿x轴正方向射出，恰好从坐标原点O进入磁场，从P（2L，0）点射出磁场．不计粒子重力，求：
（1）电场强度与磁感应强度大小之比．
（2）粒子在磁场与电场中运动时间之比．

Answer 1

分析：（1）带电粒子在电场中做类平抛运动，进入磁场后做圆周运动，对两过程由牛顿运动定律可得出关于电场强度和磁感应强度的表达式，则可求得二者的比值；
（2）由平抛运动规律可得出粒子在电场中的时间，由圆周的性质可得出粒子在磁场中的运动时间．

解答：解：由平抛运动规律及牛顿运动定律得
2L=v₀t₁
L=

1

2

at₁²
Eq=ma
粒子到达O点时沿+y方向分速度v_y=at₁=v₀
tanα=

vy

v0

=45°
粒子在磁场中的速度为v=

2

v₀
因洛仑兹力充当向心力，即Bqv=m

v2

r

由几何关系可知r=

2

L
联立可得：

E

B

=

V0

2

（2）粒子在磁场中运动的周期T=

2πr

v

粒子在磁场中运动的时间t₂=

1

4

T=

πL

2v0

则磁场与电场中运动时间之比：

t2

t1

=

π

4

；

点评：带电粒子在匀强电场中运动时，要注意应用运动的合成和分解；而在磁场中运动时为匀速圆周运动，在解题时要注意应用好平抛和圆周运动的性质．