题目内容
1.某物体做匀变速直线运动的位移跟时间的关系是s=2t2+$\frac{1}{2}$t(式中s的单位是 m,t的单位是s),则当物体的初速度大小为$\frac{1}{2}$m/s,物体的加速度为4 m/s2.分析 根据匀变速直线运动的公式$x={v}_{0}^{\;}t+\frac{1}{2}a{t}_{\;}^{2}$去分析初速度和加速度
解答 解:根据$x={v}_{0}^{\;}t+\frac{1}{2}a{t}_{\;}^{2}$以及$s=2{t}_{\;}^{2}+\frac{1}{2}t$
知${v}_{0}^{\;}=\frac{1}{2}m/s$
$\frac{1}{2}a=2$,即$a=4m/{s}_{\;}^{2}$
故答案为:$\frac{1}{2}$ 4
点评 解决本题的关键掌握匀变速直线运动的位移时间公式$x={v}_{0}^{\;}t+\frac{1}{2}a{t}_{\;}^{2}$,基础题目.

练习册系列答案
相关题目
11. 把质量为m的小球放在竖直的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧处于自由状态(图乙).已知B、A的高度差为h1,C、A的高度差为h2,重力加速度为g,则( )
把质量为m的小球放在竖直的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧处于自由状态(图乙).已知B、A的高度差为h1,C、A的高度差为h2,重力加速度为g,则( )
 把质量为m的小球放在竖直的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧处于自由状态(图乙).已知B、A的高度差为h1,C、A的高度差为h2,重力加速度为g,则( )
把质量为m的小球放在竖直的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧处于自由状态(图乙).已知B、A的高度差为h1,C、A的高度差为h2,重力加速度为g,则( )| A. | 状态甲中弹簧的弹性势能为mgh2 | |
| B. | 小球由状态甲到状态乙的过程中速度一直增大 | |
| C. | 小球由状态甲到状态乙的过程中机械能守恒 | |
| D. | 状态乙中小球的动能最大 |
12.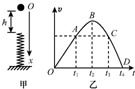 蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚开始下落计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法中正确的是( )
蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚开始下落计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法中正确的是( )
 蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚开始下落计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法中正确的是( )
蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚开始下落计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法中正确的是( )| A. | 下落h高度时小球速度最大 | |
| B. | 小球在t4时刻所受弹簧弹力大于2mg | |
| C. | t2-t1>t3-t2 | |
| D. | 球在t1到t4的时间内重力势能减小量大于弹簧弹性势能的增加量 |
10.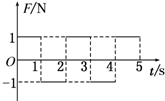 一个静止的质点,在0~5s时间内受到合力F的作用,合力的方向始终在同一直线上,合力F随时间t的变化图线如图所示.则质点在( )
一个静止的质点,在0~5s时间内受到合力F的作用,合力的方向始终在同一直线上,合力F随时间t的变化图线如图所示.则质点在( )
 一个静止的质点,在0~5s时间内受到合力F的作用,合力的方向始终在同一直线上,合力F随时间t的变化图线如图所示.则质点在( )
一个静止的质点,在0~5s时间内受到合力F的作用,合力的方向始终在同一直线上,合力F随时间t的变化图线如图所示.则质点在( )| A. | 第1s末速度方向改变 | B. | 第2s末前后加速度方向不变 | ||
| C. | 第4s末运动速度为零 | D. | 第4s末回到原出发点 |
11.比较下列各物理量的大小时,正确的结论是( )
| A. | 电量:+2×10-8库仑>-3×10-8库仑 | |
| B. | 场强:+500牛顿/库仑>-800牛顿/库仑 | |
| C. | 电势:+60伏<-80伏 | |
| D. | 电势能:+48焦>-56焦 |
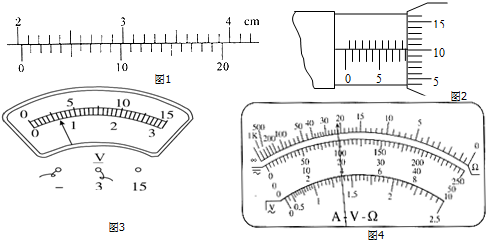
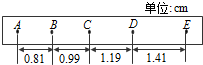 在“探究小车速度随时间变化规律”的实验中,打点计时器在纸带上依次打出一系列的点A、B、C、D、E、…,相邻两点间的距离如右图所示,计时器打点周期为0.02s,则打C点时的瞬间,纸带的速度大小为0.545m/s;纸带的加速度为5m/s2.
在“探究小车速度随时间变化规律”的实验中,打点计时器在纸带上依次打出一系列的点A、B、C、D、E、…,相邻两点间的距离如右图所示,计时器打点周期为0.02s,则打C点时的瞬间,纸带的速度大小为0.545m/s;纸带的加速度为5m/s2. 如图所示,物体A的质量为2m,物体B的质量为m,A与地面的动摩擦因数为μ,B与地面的摩擦不计,用水平力F向右推A使A、B一起加速运动,求:
如图所示,物体A的质量为2m,物体B的质量为m,A与地面的动摩擦因数为μ,B与地面的摩擦不计,用水平力F向右推A使A、B一起加速运动,求:


