题目内容
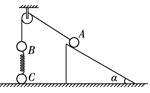
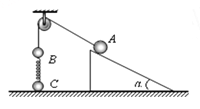
【题目】如图所示是一皮带传输装载机械的示意图.井下挖掘工将矿物无初速度地放置于沿图示方向运行的传送带A端,被传输到末端B处,再沿一段圆形轨道到达轨道的最高点C处,然后水平抛到货台上.已知半径为R=0.4m的圆形轨道与传送带在B点相切,O点为半圆的圆心,BO、CO分别为圆形轨道的半径,矿物m可视为质点,传送带与水平面间的夹角θ=37°,矿物与传送带间的动摩擦因数μ=0.8,传送带匀速运行的速度为v0=5m/s,传送带AB点间的长度为sAB=45m.若矿物落点D处离最高点C点的水平距离为xCD=2m,竖直距离为hCD=1.25m,矿物质量m=50kg,sin 37°=0.6,cos 37°=0.8,g取10m/s2,不计空气阻力.求:
(1)矿物到达B点时的速度大小;
(2)矿物到达C点时对轨道的压力大小;
(3)皮带对矿物做了多少功.

【答案】(1)5m/s;(2)1500N;(3)14215J
【解析】(1)假设矿物在AB段始终处于加速状态,由动能定理可得:
(μmgcosθ-mgsinθ)sAB=![]() mvB2
mvB2
代入数据得:vB=6m/s
由于vB>v0=5m/s,故假设不成立,说明传送带先加速与传送带共速后然后匀速运动,则矿物B处速度为5m/s.
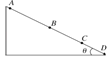
(2)设矿物对轨道C处压力为F,由平抛运动知识可得:
sCD=vCt
hCD=![]() gt2
gt2
代入数据得矿物到达C处时速度为:vC=4m/s
由牛顿第二定律可得: ![]()
代入数据得:F=1500N
根据牛顿第三定律可得所求压力为:F′=F=1500N
(3)依动能定理WAB=△EK 有:-mgSAB sin370 +W带=![]() mvB2-0
mvB2-0
解得:W带=14215J

练习册系列答案
相关题目