题目内容
18. 如图所示,甲、乙、丙三个相同的小物块(可视为质点)质量均为m,将两个不同的轻质弹簧压缩到最紧并用轻绳固定,弹簧与小物块之间不连接,整个系统静止在光滑水平地面上,甲物块距离左边墙壁距离为l(l远大于弹簧的长度),某时刻烧断甲乙之间的轻绳,甲与乙、丙之间的连接绳瞬间断开,经过时间t,甲与墙壁发生弹性碰撞,与此同时乙、丙之间的连接绳瞬间断开,又经过时间$\frac{t}{2}$,甲与乙发生第一次碰撞,设所有碰撞均为弹性碰撞,弹簧弹开后不再影响甲、乙、丙的运动,求:
如图所示,甲、乙、丙三个相同的小物块(可视为质点)质量均为m,将两个不同的轻质弹簧压缩到最紧并用轻绳固定,弹簧与小物块之间不连接,整个系统静止在光滑水平地面上,甲物块距离左边墙壁距离为l(l远大于弹簧的长度),某时刻烧断甲乙之间的轻绳,甲与乙、丙之间的连接绳瞬间断开,经过时间t,甲与墙壁发生弹性碰撞,与此同时乙、丙之间的连接绳瞬间断开,又经过时间$\frac{t}{2}$,甲与乙发生第一次碰撞,设所有碰撞均为弹性碰撞,弹簧弹开后不再影响甲、乙、丙的运动,求:(Ⅰ)乙丙之间连接绳断开前瞬间乙、丙连接体的速度大小?
(Ⅱ)乙、丙之间弹簧初始时具有的弹性势能.
分析 (Ⅰ)乙丙之间连接绳断开前瞬间甲与乙、丙连接体的在水平方向的动量守恒,结合l=v0t即可求出它们的速度大小;
(Ⅱ)乙、丙分离前后在水平方向满足动量守恒定律,然后结合功能关系即可求出开始时弹簧具有的弹性势能.
解答 解:( I)甲与乙丙连接体分离时的速度大小为$\frac{l}{t}$
设乙丙连接体在分离前瞬间的速度大小为v,选择向右为正方向,则:$2mv-m•\frac{l}{t}=0$
解得:$v=\frac{l}{2t}$
( II)乙与丙分离时,它们的位移:$x=vt=\frac{l}{2t}×t=\frac{1}{2}l$
设乙丙分离后乙的速度大小为v乙,丙的速度大小为v丙
则甲与乙相遇时满足:$l+\frac{l}{2}=(\frac{l}{t}+{v}_{乙})•\frac{t}{2}$
分离前后乙丙组成的系统动量守恒,乙向右为正方向,则:2mv=mv乙+mv丙
乙、丙之间弹簧初始时具有的弹性势能:
${E}_{P}=\frac{1}{2}m{v}_{乙}^{2}+\frac{1}{2}m{v}_{丙}^{2}-\frac{1}{2}•2m{v}^{2}$
联立以上方程,解得:${E}_{P}=\frac{25m{l}^{2}}{4{t}^{2}}$
答:(Ⅰ)乙丙之间连接绳断开前瞬间乙、丙连接体的速度大小是$\frac{l}{2t}$;
(Ⅱ)乙、丙之间弹簧初始时具有的弹性势能是$\frac{25m{l}^{2}}{4{t}^{2}}$.
点评 该题考查多个物体的动量守恒定律,涉及的过程比较多,要注意对过程的把握,分析清楚各过程中 的物理量之间的关系,然后再列式.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
9. 如图所示,在场强为E的匀强电场中,有一个带电荷量为q的正电荷,从A点移到B点,设AB连线与电场线平行,A、B间距离为d,则可知此电荷在此过程中的( )
如图所示,在场强为E的匀强电场中,有一个带电荷量为q的正电荷,从A点移到B点,设AB连线与电场线平行,A、B间距离为d,则可知此电荷在此过程中的( )
 如图所示,在场强为E的匀强电场中,有一个带电荷量为q的正电荷,从A点移到B点,设AB连线与电场线平行,A、B间距离为d,则可知此电荷在此过程中的( )
如图所示,在场强为E的匀强电场中,有一个带电荷量为q的正电荷,从A点移到B点,设AB连线与电场线平行,A、B间距离为d,则可知此电荷在此过程中的( )| A. | 电场力做正功,电势能增加 | B. | 电场力做正功,电势能减少 | ||
| C. | 电场力做负功,电势能增加 | D. | 电场力做负功,电势能减少 |
6.利用电流表和电压表测定一节干电池的电动势和内电阻的电路如图1.图2是实验室已有电流表和电压表表盘,要求尽量减小实验误差.现有两种规格的滑动变阻器 A.滑动变阻器(0~50Ω). B.滑动变阻器(0~200Ω),开关和导线随意选.

(1)实验中滑动变阻器应选用A.(选填相应器材前的字母)
(2)某位同学记录的6组数据如表所示,其中5组数据的对应点已经标在图3的坐标纸上,请标出余下一组数据的对应点,并画出U-I图线.
(3)根据(2)中所画图线可得出干电池的电动势E=1.5V,内电阻r=0.83Ω.
(4)实验中,随着滑动变阻器滑片的移动,电压表的示数U及干电池的输出功率P都会发生变化.定性画出PU关系的关系曲线(图4).(用E、r为已知量,标出图线与坐标轴交点坐标和极值点坐标)


(1)实验中滑动变阻器应选用A.(选填相应器材前的字母)
(2)某位同学记录的6组数据如表所示,其中5组数据的对应点已经标在图3的坐标纸上,请标出余下一组数据的对应点,并画出U-I图线.
| 序号 | 电压 U(V) | 电流 I (A) |
| 1 | 1.45 | 0.06 |
| 2 | 1.40 | 0.12 |
| 3 | 1.30 | 0.24 |
| 4 | 1.25 | 0.26 |
| 5 | 1.20 | 0.36 |
| 6 | 1.10 | 0.48 |
(4)实验中,随着滑动变阻器滑片的移动,电压表的示数U及干电池的输出功率P都会发生变化.定性画出PU关系的关系曲线(图4).(用E、r为已知量,标出图线与坐标轴交点坐标和极值点坐标)

13.已知地球半径为R,质量为M,自转周期为T,在赤道处用弹簧秤悬挂某物体(质量为m),静止时示数为F,万有引力常量为G,下列说法正确的是( )
| A. | 在北极进行同样的操作,弹簧秤示数依然是F | |
| B. | 在赤道处重力的大小等于F,且F=G$\frac{Mm}{{R}^{2}}$-m$\frac{4{π}^{2}}{{T}^{2}}$R | |
| C. | 假如地球自转周期减小,那么赤道上物体的重力也减小 | |
| D. | 地球的第一宇宙速度v1=$\frac{2πR}{T}$ |
3.现要测量一个未知电阻Rx的阻值,除Rx外可用的器材有:
多用电表(仅可使用欧姆档) 电池组(电动势为3V,内阻为1Ω) 电流表(内阻约0.1Ω) 电压表(内阻约3kΩ) 滑动变阻器R(0~20Ω,额定电流2A)、开关、导线若干.
(1)先用多用电表的欧姆挡粗测未知电阻,采用“×10”挡,调零后测量该电阻,发现指针偏转非常大,下列判断和做法正确的是AC(填字母代号).
A.这个电阻阻值很小,估计只有几欧姆
B.这个电阻阻值很大,估计有几千欧姆
C.如需进一步测量可换“×1”挡,调零后测量
D.如需进一步测量可换“×1k”挡,调零后测量
(2)某小组同学用伏安法测该电阻Rx.利用以上器材正确连接好电路,进行实验测量,记录数据如下:
由以上数据可知,他们测量Rx是采用图1中的甲图(选填“甲”或“乙”).

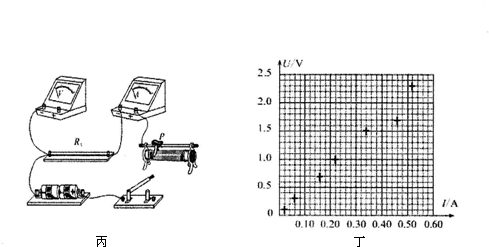
(3)如图丙是测量Rx的实验器材实物图,图中已连接了部分导线,滑动变阻器的滑片P置于变阻器的一端.请根据(2)中所选电路图,补充完成图丙中实物间的连线,并使用闭合开关的瞬间,电压表或电流表不至于被烧坏.
(4)这个小组的同学在坐标纸上建立U、I坐标系,如图丁所示,图中已标出了测量数据对应的7个坐标点.请在图中描绘出U-I图线.由图线得到金属丝的阻值Rx=4.5Ω(保留两位有效数字)
多用电表(仅可使用欧姆档) 电池组(电动势为3V,内阻为1Ω) 电流表(内阻约0.1Ω) 电压表(内阻约3kΩ) 滑动变阻器R(0~20Ω,额定电流2A)、开关、导线若干.
(1)先用多用电表的欧姆挡粗测未知电阻,采用“×10”挡,调零后测量该电阻,发现指针偏转非常大,下列判断和做法正确的是AC(填字母代号).
A.这个电阻阻值很小,估计只有几欧姆
B.这个电阻阻值很大,估计有几千欧姆
C.如需进一步测量可换“×1”挡,调零后测量
D.如需进一步测量可换“×1k”挡,调零后测量
(2)某小组同学用伏安法测该电阻Rx.利用以上器材正确连接好电路,进行实验测量,记录数据如下:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 0.10 | 0.30 | 0.70 | 1.00 | 1.50 | 1.70 | 2.30 |
| I/A | 0.020 | 0.060 | 0.160 | 0.220 | 0.340 | 0.460 | 0.520 |

(3)如图丙是测量Rx的实验器材实物图,图中已连接了部分导线,滑动变阻器的滑片P置于变阻器的一端.请根据(2)中所选电路图,补充完成图丙中实物间的连线,并使用闭合开关的瞬间,电压表或电流表不至于被烧坏.
(4)这个小组的同学在坐标纸上建立U、I坐标系,如图丁所示,图中已标出了测量数据对应的7个坐标点.请在图中描绘出U-I图线.由图线得到金属丝的阻值Rx=4.5Ω(保留两位有效数字)

8. 如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点).A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块A和B随着圆盘转动时,始终与圆盘保持相对静止.则在圆盘转动的角速度从0缓慢增大的过程中,下列说法正确的是( )
如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点).A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块A和B随着圆盘转动时,始终与圆盘保持相对静止.则在圆盘转动的角速度从0缓慢增大的过程中,下列说法正确的是( )
 如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点).A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块A和B随着圆盘转动时,始终与圆盘保持相对静止.则在圆盘转动的角速度从0缓慢增大的过程中,下列说法正确的是( )
如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点).A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块A和B随着圆盘转动时,始终与圆盘保持相对静止.则在圆盘转动的角速度从0缓慢增大的过程中,下列说法正确的是( )| A. | B所受合外力一直等于A所受合外力 | |
| B. | A受到的摩擦力一直指向圆心 | |
| C. | B受到的摩擦力一直指向圆心 | |
| D. | A、B两物块与圆盘保持相对静止的最大角速度为$\sqrt{\frac{{2{f_m}}}{mR}}$ |
 模拟交通路口电子警察的电路如图所示,当红灯亮起时,触发S2闭合;再有汽车越过路口斑马线时,触发S1闭合;启动摄像仪对汽车违章进行拍摄.能实现此功能的逻辑门电路是( )
模拟交通路口电子警察的电路如图所示,当红灯亮起时,触发S2闭合;再有汽车越过路口斑马线时,触发S1闭合;启动摄像仪对汽车违章进行拍摄.能实现此功能的逻辑门电路是( )



 如图所示,小球的质量为m=2.0kg,在光滑的水平面上以速度v1=10m/s向竖直的墙面运动,与墙面相碰后弹回,速度变为v2=5,求物体的动量的改变量大小和方向,若小球与墙壁作用的时间为0.01s,小球对墙壁的平均冲力为多少?
如图所示,小球的质量为m=2.0kg,在光滑的水平面上以速度v1=10m/s向竖直的墙面运动,与墙面相碰后弹回,速度变为v2=5,求物体的动量的改变量大小和方向,若小球与墙壁作用的时间为0.01s,小球对墙壁的平均冲力为多少? 如图所示的照片是游乐场中“激流飞下”的项目,小船在倾斜水槽中滑时阻力很小,你能依据照片提供的信息估算小船滑到底部时的速度吗?
如图所示的照片是游乐场中“激流飞下”的项目,小船在倾斜水槽中滑时阻力很小,你能依据照片提供的信息估算小船滑到底部时的速度吗?