题目内容
11.变化的磁场可以激发感生电场,电子感应加速器就是利用感生电场使电子加速的设备.它的基本原理如图所示,上、下为两个电磁铁,磁极之间有一个环形真空室,电子在真空室内做圆周运动.电磁铁线圈电流的大小、方向可以变化,在两极间产生一个由中心向外逐渐减弱、而且变化的磁场,这个变化的磁场又在真空室内激发感生电场,其电场线是在同一平面内的一系列同心圆,产生的感生电场使电子加速.图1中上部分为侧视图、下部分为俯视图.已知电子质量为m、电荷量为e,初速度为零,电子圆形轨道的半径为R.穿过电子圆形轨道面积的磁通量Φ随时间t的变化关系如图2所示,在t0 时刻后,电子轨道处的磁感应强度为B0,电子加速过程中忽略相对论效应.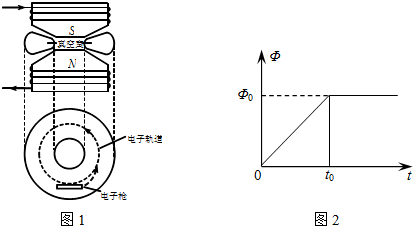
(1)求在t0 时刻后,电子运动的速度大小;
(2)求电子在整个加速过程中运动的圈数;
(3)电子在半径不变的圆形轨道上加速是电子感应加速器关键技术要求.试求电子加速过程中电子轨道处的磁感应强度随时间变化规律.
当磁场分布不均匀时,可认为穿过一定面积的磁通量与面积的比值为平均磁感应强度$\overline B$.请进一步说明在电子加速过程中,某一确定时刻电子轨道处的磁感应强度与电子轨道内的平均磁感应强度的关系.
分析 (1)电子在匀强磁场在做匀速圆周运动,洛伦兹力提供向心力,即可求出粒子运动 的速度;
(2)由动能定理求出电子获得的总动能以及电子加速一周获得的动能,二者之比即为所求;
(3)由法拉第电磁感应定律得出感生电场的大小,由牛顿第二定律求出加速度,由v=at得出速度,再结合洛伦兹力提供向心力即可得出结论.
解答 解:(1)在t0 时刻后,电子轨道处的磁感应强度为B0,电子在磁场中作匀速圆周运动,受到洛伦兹力等于向心力 $e{v_0}{B_0}=m\frac{v_0^2}{R}$
${v_0}=\frac{{e{B_0}R}}{m}$
(2)加速后电子的动能为 ${E_K}=\frac{1}{2}mv_0^2=\frac{{{e^2}B_0^2{R^2}}}{2m}$①
感生电场的感应电动势${E_感}=\frac{ϕ_0}{t_0}$②
电子加速运动一圈获得的能量为W=eE感③
电子在整个加速过程中运动的圈数为$n=\frac{{{E_K}-0}}{W}$④
联立①②③④得$n=\frac{{eB_0^2{R^2}{t_0}}}{{2m{ϕ_0}}}$
(3)感生电场的电场强度$E=\frac{E_感}{2πR}$⑤
电子加速的加速度$a=\frac{eE}{m}$⑥
t时刻电子的速度为v=at⑦
此时电子作圆周运动时受到洛伦兹力等于向心力$evB=m\frac{v^2}{R}$⑧
联立②⑤⑥⑦⑧得$B=\frac{ϕ_0}{{2π{R^2}{t_0}}}t$⑨
t时刻的电子轨道内的磁通量为$ϕ=\frac{ϕ_0}{{t_0^{\;}}}t$
t时刻的电子轨道内的平均磁感应强度为$\overline B=\frac{ϕ}{{π{R^2}}}=\frac{ϕ_0}{{π{R^2}t_0^{\;}}}t$⑩
所以由⑨⑩得,t时刻电子轨道处的磁感应强度与电子轨道内的平均磁感应强度的关系为$B=\frac{\overline{B}}{2}=\frac{{ϕ}_{0}}{2π{R}^{2}{t}_{0}}t$
答:(1)在t0 时刻后,电子运动的速度大小是$\frac{e{B}_{0}R}{m}$;
(2)电子在整个加速过程中运动的圈数是$\frac{e{B}_{0}^{2}{R}^{2}{t}_{0}}{2m{ϕ}_{0}}$;
(3)电子加速过程中电子轨道处的磁感应强度随时间变化规律是$B=\frac{{ϕ}_{0}}{2π{R}^{2}{t}_{0}}t$.
点评 该题中,以电子感应加速器利用感生电场使电子加速的原理为纽带,将带电粒子在磁场中的运动与法拉第电磁感应定律结合在一起,充分考查带电粒子在磁场中的运动的特点,以及带电粒子在电场中运动的特点,是一道理论联系实际的好题.

 如图所示,在光滑水平面上,用弹簧水平连接一斜面,弹簧的另一端固定在墙上,一人站在斜面上,最初系统静止不动,后来人沿斜面加速向上运动,则( )
如图所示,在光滑水平面上,用弹簧水平连接一斜面,弹簧的另一端固定在墙上,一人站在斜面上,最初系统静止不动,后来人沿斜面加速向上运动,则( )| A. | 最初系统静止不动时,弹簧处于压缩状态 | |
| B. | 最初系统静止不动时,斜面共受到4个力作用 | |
| C. | 在人沿斜面加速向上运动的过程中,弹簧处于压缩状态 | |
| D. | 在人沿斜面加速向上运动的过程中,弹簧处于原长 |
| A. | 气球内的气体从外界吸收了热量,内能增加 | |
| B. | 气球内的气体温度升高、体积不变、压强减小 | |
| C. | 气球内的气体压强增大,所以单位体积内的分子增加,单位面积的碰撞频率增加 | |
| D. | 气球内的气体虽然分子数不变,但分子对器壁单位时间、单位面积碰撞时的作用力增大 |
 如图所示为理想变压器,原、副线圈匝数比为2:1,原线圈接交流电压u=220sin100πtV,图中电压表和电流表为理想电表,R1为负温度系数的热敏电阻(当温度升高时阻值减小),则正确的是( )
如图所示为理想变压器,原、副线圈匝数比为2:1,原线圈接交流电压u=220sin100πtV,图中电压表和电流表为理想电表,R1为负温度系数的热敏电阻(当温度升高时阻值减小),则正确的是( )| A. | 交流电压的有效值是220V | |
| B. | 电压表示数是110V | |
| C. | 当R1处温度降低时,电压表示数不变 | |
| D. | 当R1处温度降低时,此变压器的输入功率将变小 |

| A. | 气体内每个分子动能都增大 | B. | 气体内能增加 | ||
| C. | 气体一定吸热 | D. | 气体体积可能增大 |

 如图所示,质量为m的物体A,从弧形面的底端以初速v0向上滑行,达到某一高度后,又循原路返回,且继续沿水平面滑行至P点而停止,求在整个过程中摩擦力对物体A所做的功.
如图所示,质量为m的物体A,从弧形面的底端以初速v0向上滑行,达到某一高度后,又循原路返回,且继续沿水平面滑行至P点而停止,求在整个过程中摩擦力对物体A所做的功. 如图所示,一辆拖车通过定滑轮将一重物G匀速提升,当拖车从A点水平移动到B点时,位移为s,绳子由竖直变为与竖直方向成θ的角度,求此过程中拖车对绳子所做的功.
如图所示,一辆拖车通过定滑轮将一重物G匀速提升,当拖车从A点水平移动到B点时,位移为s,绳子由竖直变为与竖直方向成θ的角度,求此过程中拖车对绳子所做的功. 在如图所示的竖直平面内,在水平线MN的下方有足够大的匀强磁场,一个等腰三角形金属线框顶点C与MN重合,线框由静止释放,沿轴线DC方向竖直落入磁场中.忽略空气阻力,从释放到线框完全进入磁场过程中,关于线框运动的v-t图,可能正确的是( )
在如图所示的竖直平面内,在水平线MN的下方有足够大的匀强磁场,一个等腰三角形金属线框顶点C与MN重合,线框由静止释放,沿轴线DC方向竖直落入磁场中.忽略空气阻力,从释放到线框完全进入磁场过程中,关于线框运动的v-t图,可能正确的是( )