题目内容
已知万有引力常量G，某行星的半径R和绕该行星表面运行的卫星的周期T，可以求得下面哪些量：
A．卫星的质量 B．该行星表面的重力加速度
C．该行星的同步卫星离其表面的高度 D．该行星的第一宇宙速度
【答案】
BD
【解析】
试题分析：根据万有引力提供向心力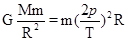
，求出行星的质量，根据
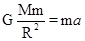，求出行星表面的重力加速度．
解：A、根据万有引力提供向心力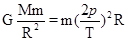，木星的质量
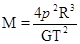．卫星是环绕天体，在运算时质量被约去，无法求出．故A错误，该行星表面的重力加速度可有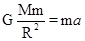求出，B正确．C、设同步卫星距地面高度为h，则：
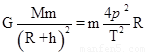不知道同步卫星的周期，没法求出高度，C错误，以第一宇宙速度运行的卫星其轨道半径就是R，则
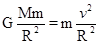求出该行星的第一宇宙速度，故D正确．
故选BD．
考点：万有引力定律及其应用．
点评：解决本题的关键掌握万有引力提供向心力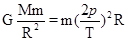．知道要求某一天体的质量，需将它放到中心天体位置．
练习册系列答案
相关题目
太阳系八大行星绕太阳运动的轨道可粗略地认为是圆，各行星的半径、日星距离和质量如下表所示：
|
| A、太阳系的八大行星中，海王星的圆周运动速率最大 |
| B、太阳系的八大行星中，水星的圆周运动周期最大 |
| C、如果已知地球的公转周期为1年，万有引力常量G=6.67×10-11Nm2/kg2，再利用地球和太阳间的距离，则可以求出太阳的质量 |
| D、如果已知万有引力常量G=6.67×10-11Nm2/kg2，并忽略地球的自转，利用地球的半径以及地球表面的重力加g=10m/s2，则可以求出太阳的质量 |