题目内容
一物体相对静止在平均密度为ρ的球形星球表面的赤道上．已知万有引力常量G，若由于星球自转使物体对星球表面压力恰好为零，则星球自转周期为多大？（已知球的体积公式为V=
πR3，R为球半径．）
| 4 | 3 |
分析：天体对物体的万有引力恰好等于物体随天体转动所需要的向心力，根据牛顿第二定律可列式解得．
解答：解：赤道表面的物体对天体表面的压力为零，说明天体对物体的万有引力恰好等于物体随天体转动所需要的向心力，
即F向=F引
F向=m(
)2R
F引=G
又M=ρ×
πR3
解以上四式，
得：ρ
=m(
)2R
整理得：T=
答：星球自转使物体对星球表面压力恰好为零，则星球自转周期为T=
．
即F向=F引
F向=m(
| 2π |
| T |
F引=G
| Mm |
| R2 |
又M=ρ×
| 4 |
| 3 |
解以上四式，
得：ρ
G
| ||
| R2 |
| 2π |
| T |
整理得：T=
|
答：星球自转使物体对星球表面压力恰好为零，则星球自转周期为T=
|
点评：本题关键抓住万有引力提供向心力，列式求解出线速度、角速度、周期和向心力的表达式，再进行讨论．
练习册系列答案
相关题目
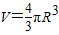，R为球半径．）