题目内容
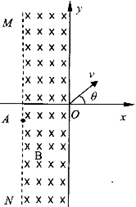
(13分)如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点。在A点有放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量均为m,电量均为q,不计重力。试求:
(1)电荷在电场中运动的加速度多大?
(2)运动轨迹经过B点的电荷在A点时的速度多大?
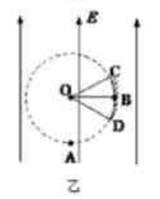
(3)若在圆形区域的边缘有一圆弧形接收屏CBD,B点仍是圆形区域最右侧的点,C、D分别为接收屏上最边缘的两点,如图乙所示,∠COB=∠BOD=37°。求该屏上接收到的电荷的末动能大小的范围。(提示:sin37°=0.6,cos37°=0.8。)
(1)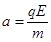 (2)vA=
(2)vA=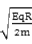
(3)最小动能为:EKD = EqR(5-3cos53°)= EqR
EqR
最大动能为:EKC= EqR(5-3cos127°)= EqR
EqR
解析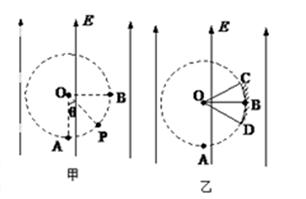
试题分析:(1)电荷在电场中受到电场力,据牛顿第二定律得: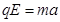
则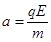
(2)电荷在电场中做平抛运动,设A点速度为vA, 则
水平方向: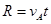
竖直方向: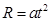
联立②③④式得:vA=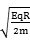
(3)设圆周上任意点P与OA成θ角,如甲图,电荷以初速度v0由A运动到P时间t0,则
水平方向:Rsinθ=v0t0
竖直方向:R-Rcosθ=at02
A点动能EKA= mv02
mv02
对电荷由A运动到P过程运用动能定理:Eq(R-Rcosθ)= EKP-EKA
立②⑥⑦⑧⑨式得:EKP = EqR(5-3cosθ)
由⑩式可知,θ角增大,EKP增大,如乙图,因此D点接收到的电荷的末动能最小,C点接收到的电荷的末动能最大。
最小动能为:EKD = EqR(5-3cos53°)=  EqR
EqR
最大动能为:EKC= EqR(5-3cos127°)=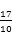 EqR
EqR
考点:本题考查牛顿第二定律、类平抛运动规律、动能定理。

 名校课堂系列答案
名校课堂系列答案 、质量为m的带电粒子以速度
、质量为m的带电粒子以速度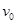 从上板边缘沿平行于板的方向射入两板间.结果粒子恰好从下板右边缘飞进磁场,然后又恰好从下板的左边缘飞进电场.不计粒子重力.试求:
从上板边缘沿平行于板的方向射入两板间.结果粒子恰好从下板右边缘飞进磁场,然后又恰好从下板的左边缘飞进电场.不计粒子重力.试求:
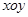 中,
中, 轴左侧有沿
轴左侧有沿 轴正向的匀强电场,场强大小为E;
轴正向的匀强电场,场强大小为E; 时刻,从
时刻,从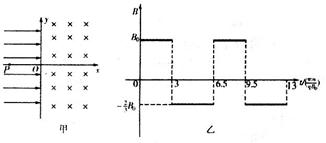
 ,虚线下方匀强磁场范围足够大,磁感应强度为
,虚线下方匀强磁场范围足够大,磁感应强度为 ,现有质量为
,现有质量为 、电量为
、电量为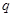 的带正电粒子从距电磁场边界
的带正电粒子从距电磁场边界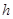 处无初速释放(带电粒子重力可忽略不计).求:
处无初速释放(带电粒子重力可忽略不计).求: 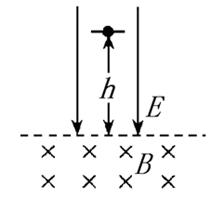
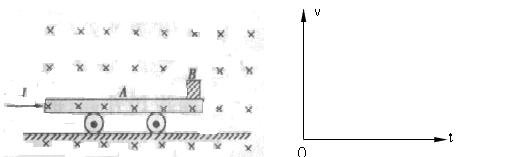
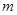 、带电量为
、带电量为 的粒子自y轴的P点沿x轴正方向射入第四象限,经x轴上的Q点进入第一象限,随即撤去电场,以后仅保留磁场。已知OP=d,OQ=2d,不计粒子重力。
的粒子自y轴的P点沿x轴正方向射入第四象限,经x轴上的Q点进入第一象限,随即撤去电场,以后仅保留磁场。已知OP=d,OQ=2d,不计粒子重力。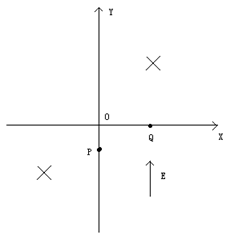

 的匀强磁场中。已知匀强电场的宽度为d=
的匀强磁场中。已知匀强电场的宽度为d= R,匀强磁场由一个长为2R、宽为
R,匀强磁场由一个长为2R、宽为
 倍。粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场。已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期。忽略重力的影响。求:
倍。粒子进入电场后,在电场力的作用下又由O点返回磁场区域,经过一段时间后再次离开磁场。已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期。忽略重力的影响。求: