题目内容
(14分)水平导轨AB固定在支架CD上,其形状、尺寸如图所示。导轨与支架的总质量M=4kg,其重心在O点,它只能绕支架C点且垂直于纸面的水平轴转动。质量m=1kg的小铁块静止于水平导轨AB的A端,现受到水平拉力F=2.5N的作用。已知小铁块和导轨之间的动摩擦因数μ=0.2。g取10m/s2,求:
(1)小铁块刚开始运动时的加速度大小?
(2)小铁块运动到离A端多远时,支架将要开始翻转?
(3)若在小铁块运动的过程中,支架始终保持静止,则拉力F作用的最长时间为多少?
(1)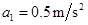 (2)
(2)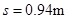 (3)
(3)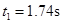
解析试题分析:(1)小铁块刚开始运动时,受到的滑动摩擦力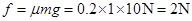
由牛顿第二定律,可得小铁块的加速度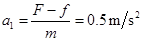
(2)假设小铁块运动到C点的右侧且距C点x处时,支架刚要不能维持平衡,D端受的力为零,
由力矩平衡条件可得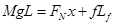
而
解得
小铁块运动到离A端的距离: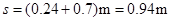
(3)因为要在小铁块运动的过程中,导轨和支架始终保持静止,故小铁块是先做匀加速直线运动,再做匀减速直线运动
匀加速阶段加速度大小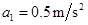
匀减速阶段加速度大小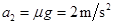
由匀变速直线运动规律,可得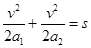
解得: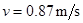
由速度-位移公式
解得: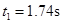
考点:本题考查了匀变速直线运动规律的应用及力矩平衡问题。

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 ,求:
,求: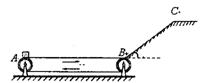


 及1.5s内物体的位移。
及1.5s内物体的位移。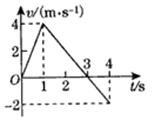
 物体的位移;
物体的位移;

 =37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,在t1=1 s时撤去拉力,物体运动的部分vt图象如图乙所示.重力加速度g取10 m/s2.
=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,在t1=1 s时撤去拉力,物体运动的部分vt图象如图乙所示.重力加速度g取10 m/s2. 。试求:
。试求: