题目内容
一行星绕恒星做圆周运动．由天文观测可得，其运行周期为
，速度为
.引力常量为
，则
A．恒星的质量为 |
B．行星的质量为 |
C．行星运动的轨道半径为 |
D．行星运动的加速度为 |
ACD
解析
名校课堂系列答案“嫦娥二号”曾飞向距离地球150万公里外的“第二拉格朗日点”（图中M），在太阳和地球引力共同作用下，“嫦娥二号”能在M点与地球一起绕太阳运动（视为圆周运动）。不考虑其他星球影响，与地球相比，“嫦娥二号”
| A．周期大 | B．角速度大 | C．线速度小 | D．向心加速度小 |
2013年12月2日，“嫦娥三号”探测器成功发射。与“嫦娥一号”的探月轨道不同，“嫦娥三号”卫星不采取多次变轨的方式，而是直接飞往月球，然后再进行近月制动和实施变轨控制，进入近月椭圆轨道。现假定地球、月球都静止不动，用火箭从地球沿地月连线向月球发射一探测器，探测器在地球表面附近脱离火箭。已知地球中心与月球中心之间的距离约为r =3．8×l05km，月球半径R=l．7×l03 km，地球的质量约为月球质量的81倍。在探测器飞往月球的过程中
| A．探测器到达月球表面时动能最小 |
| B．探测器距月球中心距离为3．8×l04 km时动能最小 |
| C．探测器距月球中心距离为3．42×l05km时动能最小 |
| D．探测器距月球中心距离为1．9×l05 km时动能最小 |
某人造地球卫星因受高空稀薄空气的阻力作用，绕地球运转的轨道会慢慢改变.每次测量中卫星的运动可近似看作圆周运动，某次测量卫星的轨道半径为r1，后来变为r2，以Ek1、Ek2表示卫星在这两个轨道上的动能，T1、T2表示卫星在这两个轨道上绕地运动的周期，则（ ）
| A．Ek2＜Ek1、T2＜T1 | B．Ek2＜Ek1、T2＞T1 |
| C．Ek2＞Ek1、T2＜T1 | D．Ek2＞Ek1、T2＞T1 |
为了探测月球，嫦娥三号探测器先在以月球中心为圆心，高度为h的圆轨道上运动，随后飞船多次变轨，最后围绕月球做近月表面的圆周飞行，周期为To引力常量G已知。则
| A．可以确定月球的质量 |
| B．可以确定月球的半径 |
| C．可以确定月球的平均密度 |
| D．可以确定嫦娥三号探测器做近月表面圆周飞行时，其质量在增大 |
美国宇航局2011年12月5日宣布，他们发现了太阳系外第一颗类似地球的、可适合居住的行星—“开普勒-22b”，它每290天环绕着一颗类似于太阳的恒星运转一周，距离地球约600光年，体积是地球的2.4倍。已知万有引力常量和地球表面的重力加速度。根据以上信息，下列推理中正确的是
| A．若能观测到该行星的轨道半径，可求出该行星所受的万有引力 |
| B．若已知该行星的密度和半径，可求出该行星的轨道半径 |
| C．根据地球的公转周期与轨道半径，可求出该行星的轨道半径 |
| D．若该行星的密度与地球的密度相等，可求出该行星表面的重力加速度 |
美国宇航局2011年12月5日宣布，他们发现了太阳系外第一颗类似地球的、可适合居住的行星—“开普勒-22b”，它每290天环绕着一颗类似于太阳的恒星运转一周，距离地球约600光年，体积是地球的2.4倍。已知万有引力常量和地球表面的重力加速度。根据以上信息，下列推理中正确的是
| A．若能观测到该行星的轨道半径，可求出该行星所受的万有引力 |
| B．若已知该行星的密度和半径，可求出该行星的轨道半径 |
| C．根据地球的公转周期与轨道半径，可求出该行星的轨道半径 |
| D．若该行星的密度与地球的密度相等，可求出该行星表面的重力加速度 |
如图所示，甲、乙两颗卫星以相同的轨道半径分别绕质量为
和
的行星做匀速圆周运动．下列说法正确的是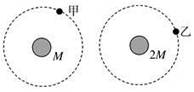 
| A．甲的向心加速度比乙的小 |
| B．甲的运行周期比乙的小 |
| C．甲的角速度比乙的大 |
| D．甲的线速度比乙的大 |