题目内容
A、B两列波在某时刻的波形如图所示，经过t=TA时间（TA为波A的周期），两波再次出现如图波形，则两波的波速之比vA：vB可能是（ ）分析：根据两图可知两波波长关系，B波经过时间t重复出现波形，说明了经历时间为其周期的整数倍，这是解本题的突破口．
解答：解：由图可知：
λA=a，
λB=a
则得λA=
a，λB=
a，λA=2λB．
根据题意周期关系为：t=TA，t=nTB（n=1、2、3…），则得TA=nTB（n=1、2、3…），
所以由v=
有：
=
，（n=1、2、3…）
当n=1时，
=2；当n=2时，
=1；当n=6时
=
由于n是整数，故
不可能为3：2．故ABC正确，D错误．
故选ABC．
| 3 |
| 4 |
| 3 |
| 2 |
则得λA=
| 4 |
| 3 |
| 2 |
| 3 |
根据题意周期关系为：t=TA，t=nTB（n=1、2、3…），则得TA=nTB（n=1、2、3…），
所以由v=
| λ |
| T |
| vA |
| vB |
| 2 |
| n |
当n=1时，
| vA |
| vB |
| vA |
| vB |
| vA |
| vB |
| 1 |
| 3 |
由于n是整数，故
| vA |
| vB |
故选ABC．
点评：波传播的是形式能量，经过整数周期将重复出现波形，这往往是解决问题的突破口．如本题中由于B波重复出现波形，说明了所经历时间为其周期整数倍．
练习册系列答案
期末集结号系列答案
相关题目
（2005?上海）A、B两列波在某时刻的波形如图所示，经过t=TA时间（TA为波A的周期），两波再次出现如图波形，则两波的波速之比vA：vB可能是（ ）
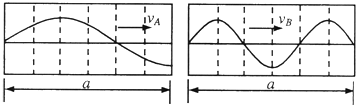
如图A、B两列波在某时刻的波形如图所示，经过t=TB时（TB为波B的周期），两波再次出现如图波形，则两波的波速之比VA：VB可能是 （ ）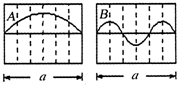
A、B两列波在某时刻的波形如图所示，经过t=TA时间（TA为波A的周期），两波再次出现如图波形，则两波的波速之比vA：vB可能是（ ）