题目内容
 (2005?上海)A、B两列波在某时刻的波形如图所示,经过t=TA时间(TA为波A的周期),两波再次出现如图波形,则两波的波速之比vA:vB可能是( )
(2005?上海)A、B两列波在某时刻的波形如图所示,经过t=TA时间(TA为波A的周期),两波再次出现如图波形,则两波的波速之比vA:vB可能是( )分析:根据两图可知两波波长关系,B波经过时间t重复出现波形,说明了经历时间为其周期的整数倍,这是解本题的突破口.
解答:解:由图可知:
λA=a,
λB=a.
根据题意周期关系为:t=TA,t=nTB(n=1、2、3…)
所以有:vA=
,vB=
(n=1、2、3…)
故有:
=
(n=1、2、3…),故选项ABD错误,C正确.
故选C.
| 3 |
| 4 |
| 3 |
| 2 |
根据题意周期关系为:t=TA,t=nTB(n=1、2、3…)
所以有:vA=
| 4a |
| 3TA |
| 2an |
| 3TA |
故有:
| vA |
| vB |
| 2 |
| n |
故选C.
点评:波传播的是形式能量,经过整数周期将重复出现波形,这往往是解决问题的突破口.如本题中由于B波重复出现波形,说明了所经历时间为其周期整数倍.

练习册系列答案
相关题目
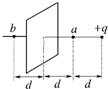 (2005?上海)如图,带电量为+q的点电荷与均匀带电薄板相距为2d,点电荷到带电薄板的垂线通过板的几何中心.若图中a点处的电场强度为零,根据对称性,带电薄板在图中b点处产生的电场强度大小为
(2005?上海)如图,带电量为+q的点电荷与均匀带电薄板相距为2d,点电荷到带电薄板的垂线通过板的几何中心.若图中a点处的电场强度为零,根据对称性,带电薄板在图中b点处产生的电场强度大小为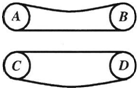 (2005?上海)对如图所示的皮带传动装置,下列说法中正确的是( )
(2005?上海)对如图所示的皮带传动装置,下列说法中正确的是( ) (2005?上海)某滑板爱好者在离地h=1.8m高的平台上滑行,水平离开A点后落在水平地面上的B点,其水平位移s1=3.6m.着地时由于存在能量损失,着地后速度变为v=4m/s,并以此为初速沿水平地面滑行s2=8m后停止.已知人与滑板的总质量m=60kg.试求:
(2005?上海)某滑板爱好者在离地h=1.8m高的平台上滑行,水平离开A点后落在水平地面上的B点,其水平位移s1=3.6m.着地时由于存在能量损失,着地后速度变为v=4m/s,并以此为初速沿水平地面滑行s2=8m后停止.已知人与滑板的总质量m=60kg.试求: