题目内容
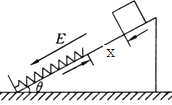
【题目】如图所示，一水平地面上固定一倾角为θ=300的光滑绝缘斜面，斜面处于电场强度为
，方向沿斜面向下的匀强电场中；一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端，整根弹簧处于自然状态．一质量为m、带电量为q（q＞0）的滑块从距离弹簧上端为x处静止释放，滑块在运动过程中电量保持不变，设滑块与弹簧接触过程没有机械能损失，弹簧始终处在弹性限度内，重力加速度大小为g．
（1）滑块从静止释放到与弹簧上端接触瞬间所经历的时间t；
（2）滑块返回的过程中，刚脱离弹簧时的速度大小；
（3）若滑块在沿斜面向下运动的整个过程中最大速度大小为vm，求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W。
【答案】（1）
（2）
（3）
【解析】
试题分析：（1）滑块从静止释放到与弹簧上端接触前，对滑块，由牛顿第二定律得：
；
滑块做初速度为零的匀加速直线运动，由位移公式得：x=
at12，
解得：
；
（2）从释放早返回由动能定理可知：
，解得
（3）当滑块速度最大时，滑块受到的合力为零，则qE+mgsinθ=kx1，
解得：
；
从滑块开始运动到速度最大过程中，由动能定理得：
（qE+mgsinθ）（x+x1）+W=
mvm2-0，
解得：
．
练习册系列答案
每课必练系列答案
相关题目
