题目内容
【题目】(1)如图1所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为m1的弹性小球从高h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为m2的弹性小球发生碰撞,碰撞前后两球的运动方向在同一水平线上,且在碰撞过程中无机械能损失。求:
a.m1球运动到B点时的速度大小v1;
b.碰撞过程中,系统的弹性势能的最大值Epm。

(2)2018年诺贝尔物理学奖授予了阿瑟·阿什金(Arthur Ashkin)等三位科学家,以表彰他们在激光领域的杰出成就。阿瑟·阿什金发明了光学镊子(如图2),能用激光束“夹起”极其微小的粒子。
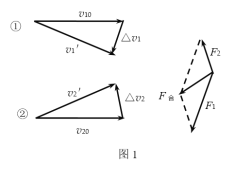
a.为了简化问题,将激光束看作是粒子流,其中的粒子以相同的动量沿光传播方向运动。激光照射到物体上,会对物体产生力的作用,光镊效应就是一个实例。现有一透明介质小球,处于非均匀的激光束中(越靠近光束中心光强越强)。小球的折射率大于周围介质的折射率。两束相互平行且强度①>②的激光束,穿过介质小球射出时的光路如图3所示。若不考虑光的反射和吸收,请分析说明两光束因折射对小球产生的合力的方向。
b.根据上问光束对小球产生的合力特点,试分析激光束如何“夹起”粒子的?

【答案】(1)a.![]() ;b.
;b.![]() (2)分析说明见解析。
(2)分析说明见解析。
【解析】
(1)a.m1从初始高度h由静止下滑,到达水平面时的速度为v1,则有:![]()
解得:![]()
b.m1球和m2球碰撞过程中,当两球速度相同时,弹性势能最大。
由动量守恒定律和机械能守恒定律得:![]()
![]()
解得:![]()
最大弹性势能![]()
(2)a.由图1可知,△v的方向即为小球对光束作用力的方向。当强度①>②强度相同时,作用力F1>F2,由平行四边形定则知,①和②光速受力合力的方向向左偏下,则由牛顿第三定律可知,两光束因折射对小球产生的合力的方向向右偏上。
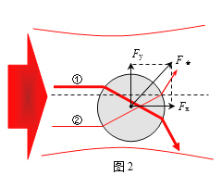
b.如图2所示,小球受到的合力向右偏上。此力的横向分力Fy,会将小球推向光束中心。一旦小球偏离光速中心,就会受到指向中心的分力,实现光束对小球的约束,如同镊子一样“夹住”小球。

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案