题目内容
水平桌面上有两个玩具车A和B,两者用一轻质细橡皮筋相连,在橡皮筋上有一红色标记R。在初始时橡皮筋处于拉直状态,A、B和R分别位于直角坐标系中的(0,2l)、(0,-l)和(0,0)点。已知A从静止开始沿y轴正向做加速度大小为a的匀加速运动:B平行于x轴朝x轴正向匀速运动。在两车此后运动的过程中,标记R在某时刻通过点(l, l)。假定橡皮筋的伸长是均匀的,求B运动速度的大小。

由题意画出xOy坐标轴及A、B位置,设B车的速度为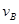 ,此时A、B的位置分别为H、G,H的纵坐标为分别为yA,G的横坐标为xB,则
,此时A、B的位置分别为H、G,H的纵坐标为分别为yA,G的横坐标为xB,则

 ①
①
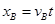 ②
②
在开始运动时R到A和B距离之比为2:1,即
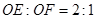
由于橡皮筋的伸长是均匀的,所以在以后任意时刻R到A和B的距离之比都为2:1。因此,在时刻t有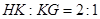 ③
③
由于 ,有
,有 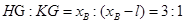 ④
④
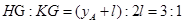 ⑤
⑤
所以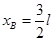 ⑥
⑥ 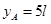 ⑦
⑦
联立①②⑥⑦解得 ⑧
⑧
【点评】本题的解题关键是橡皮筋的伸长是均匀的,由三角形的相似对应边成比例,,分别解出A、B的位置yA,xB,再由A、B各自的运动,列出方程 ①,
①,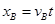 ② 就可求解
② 就可求解 。难度中等偏上,考生若是不能分析出橡皮筋的均匀伸长的特定的比值关系,仅能得①②两式的少部分分。
。难度中等偏上,考生若是不能分析出橡皮筋的均匀伸长的特定的比值关系,仅能得①②两式的少部分分。
【考点定位】匀加速直线直线运动、匀速直线运动。
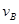 ,此时A、B的位置分别为H、G,H的纵坐标为分别为yA,G的横坐标为xB,则
,此时A、B的位置分别为H、G,H的纵坐标为分别为yA,G的横坐标为xB,则
 ①
①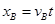 ②
②在开始运动时R到A和B距离之比为2:1,即
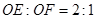
由于橡皮筋的伸长是均匀的,所以在以后任意时刻R到A和B的距离之比都为2:1。因此,在时刻t有
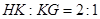 ③
③由于
 ,有
,有 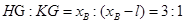 ④
④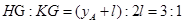 ⑤
⑤所以
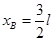 ⑥
⑥ 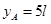 ⑦
⑦联立①②⑥⑦解得
 ⑧
⑧【点评】本题的解题关键是橡皮筋的伸长是均匀的,由三角形的相似对应边成比例,,分别解出A、B的位置yA,xB,再由A、B各自的运动,列出方程
 ①,
①,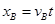 ② 就可求解
② 就可求解 。难度中等偏上,考生若是不能分析出橡皮筋的均匀伸长的特定的比值关系,仅能得①②两式的少部分分。
。难度中等偏上,考生若是不能分析出橡皮筋的均匀伸长的特定的比值关系,仅能得①②两式的少部分分。【考点定位】匀加速直线直线运动、匀速直线运动。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目




 的值减小
的值减小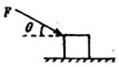
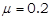 。物块A、B质量mA=mB=1kg。开始时A、B静止,A、B间压缩一轻质弹簧,蓄有弹性势能Ep=16J。现解除锁定,弹开A、B,弹开后弹簧掉落,对A、B此后的运动没有影响。g=10m/s2,求:
。物块A、B质量mA=mB=1kg。开始时A、B静止,A、B间压缩一轻质弹簧,蓄有弹性势能Ep=16J。现解除锁定,弹开A、B,弹开后弹簧掉落,对A、B此后的运动没有影响。g=10m/s2,求: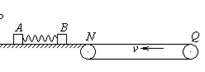
 :1
:1 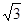 D.
D.