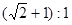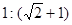题目内容
如图所示,光滑水平面MN上放两相同小物块A、B,右端N处与水平传送带理想连接,传送带水平部分长度L=8m,沿逆时针方向以恒定速度v =2m/s匀速转动。物块A、B(大小不计)与传送带间的动摩擦因数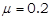 。物块A、B质量mA=mB=1kg。开始时A、B静止,A、B间压缩一轻质弹簧,蓄有弹性势能Ep=16J。现解除锁定,弹开A、B,弹开后弹簧掉落,对A、B此后的运动没有影响。g=10m/s2,求:
。物块A、B质量mA=mB=1kg。开始时A、B静止,A、B间压缩一轻质弹簧,蓄有弹性势能Ep=16J。现解除锁定,弹开A、B,弹开后弹簧掉落,对A、B此后的运动没有影响。g=10m/s2,求:
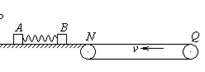
(1)物块B沿传送带向右滑动的最远距离;
(2)物块B从滑上传送带到回到水平面所用的时间。
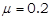 。物块A、B质量mA=mB=1kg。开始时A、B静止,A、B间压缩一轻质弹簧,蓄有弹性势能Ep=16J。现解除锁定,弹开A、B,弹开后弹簧掉落,对A、B此后的运动没有影响。g=10m/s2,求:
。物块A、B质量mA=mB=1kg。开始时A、B静止,A、B间压缩一轻质弹簧,蓄有弹性势能Ep=16J。现解除锁定,弹开A、B,弹开后弹簧掉落,对A、B此后的运动没有影响。g=10m/s2,求:
(1)物块B沿传送带向右滑动的最远距离;
(2)物块B从滑上传送带到回到水平面所用的时间。
(1)4m(2)4.5s
试题分析:(1)解锁过程动量、能量守恒:
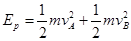
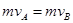
得:
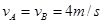
B向右作减速运动:
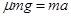 得
得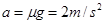
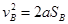 得
得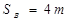
(2)B向右匀减速时间:
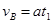 得
得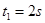
B向左加速等于传送到速度时,由
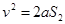 得
得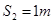
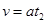 得
得
B木块与传送带共速一起向左匀速运动:
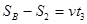 得
得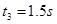 )
)总时间:
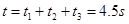
点评:本题考查了经典的传送带问题,要通过匀变速规律判断出相对运动的位移,通过能量守恒定律列式求解。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
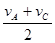 ,则
,则