Question

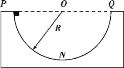
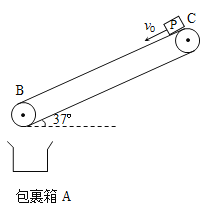
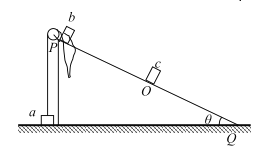
【题目】如图，倾角θ=37°的直角斜面体固定在地面上，质量为3m 的物块 c 恰好静止在斜面上的O点，质量为 M 的物块 a 和质量为m 的物块 b 通过一根不可伸长的轻绳相连，轻绳绕过斜面顶端的小滑轮并处于松驰状态，物块a 静止在地面上。从斜面顶端 P 静止释放物块 b，b 滑到 O 点前的瞬间，轻绳恰好伸直，随后瞬间绷断，a 获得 1m/s 的速度（方向竖直向上），之后 b 与 c 立即发生弹性碰撞，碰后 b 运动 1s 至斜面底端 Q。已知，物块 b 与斜面体的动摩擦因数为，空气阻力、滑轮处的摩擦均不计，取 g =10 m/s2 。求：

（1）绳伸直前的瞬间物块 b 的速度大小；

（2）轻绳绷断后，物块 b 在斜面上运动的路程；

（3）物块 a、b 的质量之比

Answer 1

【答案】（1）4.5m/s；（2）m；（3）

【解析】

（1）设b沿斜面下滑过程加速度为、绳伸直前的瞬间物块b的速度为，有

①

②

联立①②解得

m/s2

m/s

（2）设c、b碰撞后的瞬间b速度大小为，上滑的加速度为、时间为t、路程为s1，在上滑过程有

③

④

⑤

在下滑过程有

⑥

联立①～⑥解得

=﹣18m/s(舍去)

=2m/s

m

轻绳绷断后，b物块b在斜面上运动的路程

m

（3）设b、c碰撞前的瞬间b速度大小为，b、c碰撞后的瞬间速度分别为、

对b、c碰撞，取沿斜面向下为正方向

满足

⑦

⑧

联立解得

(沿斜面向上)

（沿斜面向下）

将=2m/s代入上式解得

m/s

轻绳绷断的瞬间，对b由动量定理得

⑨

对a由动量定理得

⑩

联立⑨⑩解得