题目内容
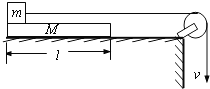
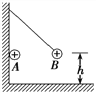
【题目】一水平传送带以4 m/s的速度逆时针传送，水平部分长L＝6 m，其左端与一倾角为θ＝30°的光滑斜面平滑相连，斜面足够长，一个可视为质点的物块无初速度地放在传送带最右端，已知物块与传送带间动摩擦因数μ＝0.2，g＝10 m/s2.求物块从放到传送带上到第一次滑回传送带最远端所用的时间．
【答案】6.1 s.
【解析】
对无初速放上传送带的物块受力分析，求出物块的加速度。计算当物块速度与传送带速度相等时，物块滑过的距离，判断物块在传送带上向左运动的过程，求出物块在传送带上向左运动的时间。物块滑上光滑斜面后，做匀变速直线运动直至返回斜面底端，据牛顿运动定律求出物块在斜面上运动的加速度，再据运动学公式求出物块在斜面上的运动时间。物块向右滑上传送带后，做减速运动，速度减为零时第一次滑回传送带最远端，对这一过程应用牛顿运动定律和运动学公式求得物块向右减速的时间。将以上三段时间相加可得物块从放到传送带上到第一次滑回传送带最远端所用的时间。
对无初速放上传送带的物块受力分析，根据牛顿第二定律得
，解得：
设物块经过位移
后与皮带速度相等，则
，解得：
，则物块在传送带上向左运动时先加速后匀速。
向左加速的时间
向左匀速的时间
对物块在斜面上时受力分析，由牛顿第二定律可得：
，解得：物块在斜面上的加速度
物块在斜面上的时间
物块返回传送带在传送带减速到零的时间
则物块从放到传送带上到第一次滑回传送带最远端所用的时间
练习册系列答案
相关题目
