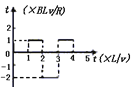
题目内容
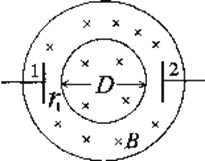
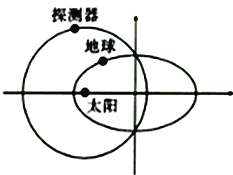
【题目】众所周知，地球绕日运动其实是一个椭圆，设其半长轴为
。如图所示，在地上发射一个绕日做圆周运动的无动力探测器，使其具有与地球相等的绕日运动周期，以便法身一年后与地球相遇而向地球发回探测资料。已知探测器发射过程可视为“在地球处给探测器一个很大的初速度，令其直接进入绕日轨道”，将地球、探测器、太阳都视为质点，且不考虑地球和其他行星对探测器运动的影响，下列说法正确的是
A. 探测器绕日运动的轨道半径等于
B. 地球在远日点的加速度大于探测器的加速度
C. 地球与探测器每次相遇时，地球位于椭圆轨道的短轴端点
D. “日地连线”单位时间扫过的面积等于“日器连线” 单位时间扫过的面积
【答案】AC
【解析】根据开普勒第三定律
，两者绕太阳的周期相同，故探测器绕日运动的轨道半径等于
，A正确；根据
可得
，地球在远日点的轨道半径大于探测器的轨道半径，故地球在远日点的加速度小于探测器的加速度，B错误；探测器离太阳的距离刚好也是长轴的一半的，换一句话说，探测器的圆形轨道与地球的椭圆轨道交点就在椭圆的短轴的端点，故两者相遇必在球位于椭圆轨道的短轴端点，C正确；根据开普勒第二定律，同一个行星在相同时间内，与太阳的连线扫过的面积相同，不同行星，相同时间内扫过的面积不同，D错误。
练习册系列答案
相关题目
