题目内容
【题目】如图所示,一个圆柱形水桶的底面半径和高相等,在其底部的正中间O点有一个点光源,在水桶内加入一定深度的水后,从水面上A点射出的光,恰好经过水桶口边缘的D点。已知BC为水桶直径,BA:AC=5:2,DC:CE=3:4。求:
(1)水对该单色光的折射率;
(2)若在水面上放置一遮光圆盘,圆盘的中心始终在O点正上方,使点光源发出的光无论照射到水面上任何位置,都不能射出水面,求该遮光圆盘的面积至少应为水面面积的多少倍?(结果保留两位有效数字)

【答案】(1)![]() (2)0.42
(2)0.42
【解析】
考查光的折射和全反射。
(1)光路图如图所示:
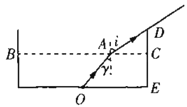
设水桶的半径为R,则有:
![]() ,
,![]() ,
,![]()
设光的折射角为i,入射角为![]() ,则有:
,则有:
![]()
![]()
由折射定律:
![]()
解得:![]() ;
;
(2)由题意,当点光源发出的光照射到水面发生全反射时,光不在射出水面。设光线入射到![]() 点时恰好发生全反射,则有:
点时恰好发生全反射,则有:
![]()
设光线在水面恰好发生全反射的位置到O点的水平距离为x,则有:
![]()
所以遮光圆盘的面积至少应为:
![]()
遮光圆盘的面积与水面面积之比为:
![]()
联立解得:![]() ,
,
即遮光圆盘的面积至少应为水面面积的0.42倍。

练习册系列答案
相关题目