题目内容
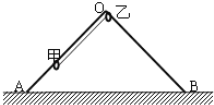
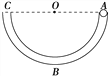
【题目】如图所示，在竖直放置的光滑半圆弧绝缘细管的圆心O处固定一点电荷，将质量为m、带电荷量为＋q的小球从圆弧管的水平直径端点A由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力．
(1)求固定于圆心处的点电荷在AB弧中点处的电场强度大小；
(2)若把O处固定的点电荷拿走，加上一个竖直向下、电场强度为E的匀强电场，带电小球仍从A点由静止释放，下滑到最低点B时，小球对环的压力多大？
【答案】（1）
（2）3(mg＋qE)．
【解析】(1)由A到B，电场力不做功，只有重力做功，由动能定理得： mgR＝
mv12，
在B点，对小球由牛顿第二定律得：qE－mg＝m
，
联立以上两式解得： E＝
.
由于是点电荷形成的电场，AB是点电荷为圆心的圆弧，故AB弧中点的电场强度为
(2)设小球到达B点时的速度为v，由动能定理得：(mg＋qE)·r＝
mv2，①
在B点处小球对环的弹力为N，由牛顿第二定律得：N－mg－qE＝m
，②
联立①和②式，解得小球在B点受到环的支持力为：N＝3(mg＋qE)，
由牛顿第三定律得：小球在B点对环的压力大小为N＝3(mg＋qE)．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
