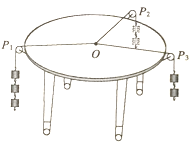
题目内容
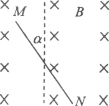
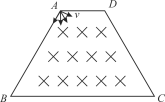
【题目】如图所示,坐标系xOy处于竖直平面内,在x>0的区域内有电场强度大小为E、方向竖直向上的匀强电场,在x>x0的区域内另有一方向垂直于坐标平面向外的匀强磁场(图中未画出)。从x轴上x=3L的P点以速度v沿y轴负方向射出的带电粒子,恰能做匀速圆周运动,运动一段时间后经过原点O,并沿与x轴负方向成θ=30°角方向射入第Ⅱ象限内,在第Ⅱ象限内加一方向平行于xOy平面的匀强电场,使粒子在第Ⅱ象限内做直线运动,已知重力加速度为g。求:
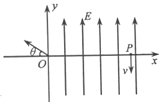
(1)x0的值;
(2)磁场的磁感应强度B;
(3)第Ⅱ象限内匀强电场的电场强度的最小值和方向。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,方向竖直向上。
,方向竖直向上。
【解析】
(1)由几何知识求解x0;(2)带电粒子在复合场做匀速圆周运动,说明电场力与重力平衡,根据粒子运动半径求出B的大小;(3)根据力的平衡原理求解最小电场强度。
(1)如右图所示:
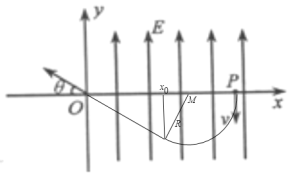
根据几何知识得:OP=3L=x0+sinθR+R,
OP=![]() +R=3R
+R=3R
联立求解得x0=![]() ,R=L
,R=L
(2)粒子做圆周运动的半径:R=![]()
又qE=mg
联立解得:B=![]()
(3)要使粒子在第Ⅱ象限内做直线运动,则电场力与重力是平衡力。
故E′q=mg
解得:E′=![]() ,方向竖直向上。
,方向竖直向上。

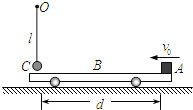
【题目】(6分)物理小组在一次探究活动中测量滑块与木板之间的动摩擦因数。实验装置如图,一表面粗糙的木板固定在水平桌面上,一端装有定滑轮;木板上有一滑块,其一端与电磁打点计时器的纸带相连,另一端通过跨过定滑轮的细线与托盘连接。打点计时器使用的交流电源的频率为50 Hz。开始实验时,在托盘中放入适量砝码,滑块开始做匀加速运动,在纸带上打出一系列小点。


(1)上图给出的是实验中获取的一条纸带的一部分:0、1、2、3、4、5、6、7是计数点,每相邻两计数点间还有4个打点(图中未标出),计数点间的距离如图所示。根据图中数据计算的加速度a= (保留三位有效数字)。
(2)回答下列两个问题:
为测量动摩擦因数,下列物理量中还应测量的有 。(填入所选物理量前的字母)
A.木板的长度l |
B.木板的质量m1 |
C.滑块的质量m2 |
D.托盘和砝码的总质量m3 |
E.滑块运动的时间t
滑块与木板间的动摩擦因数![]() = (用被测物理量的字母表示,重力加速度为g).
= (用被测物理量的字母表示,重力加速度为g).