题目内容
【题目】在如图所示的平面直角坐标系内，x轴水平、y轴竖直向下。计时开始时，位于原点处的沙漏由静止出发，以加速度a沿x轴匀加速度运动，此过程中沙从沙漏中漏出，每隔相等的时间漏出相同质量的沙。已知重力加速度为g，不计空气阻力以及沙相对沙漏的初速度。
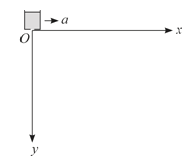
（1）求t0时刻漏出的沙在t（t> t0）时刻的位置坐标；
（2）t时刻空中的沙排成一条曲线，求该曲线方程。
【答案】
【解析】试题分析：由题意可知，沙子漏出后水平方向做匀速直线运动，竖直方向做自由落体运动，根据运动学基本公式求出在（t﹣t0）时间内水平和竖直方向的位移即可求出位置坐标，联立方程，消去未知数t0，则t时刻所有沙构成的图线方程即可求出．
解：（1）由匀变速直线运动的规律，t0时刻漏出的沙具有水平初速度
v0=at0
沙随沙漏一起匀加速的位移
接着沙平抛，t时刻位移
x1=v0（t﹣t0）
且x=x0+x1
y=
所以，t0时刻漏出的沙的坐标为：（
，
）；
（2）联立方程
，y=，消去未知数t0，则t时刻所有沙构成的图线满足方程
答：（1）t0时刻漏出的沙在t（t＞t0）时刻的位置坐标为：（
，）；
（2）该曲线方程为．
【题目】某兴趣小组利用自由落体运动测定重力加速度，实验装置如图所示。 倾斜的球槽中放有若干个小铁球，闭合开关K，电磁铁吸住第1个小球。 手动敲击弹性金属片M，M 与触头瞬间分开， 第1 个小球开始下落，M 迅速恢复，电磁铁又吸住第2 个小球．当第1 个小球撞击M 时，M 与触头分开，第2 个小球开始下落……．这样，就可测出多个小球下落的总时间．
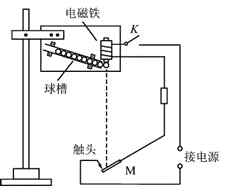
（1）在实验中，下列做法正确的有_________．
A．电路中的电源只能选用交流电源 |
B．实验前应将M 调整到电磁铁的正下方 |
C．用直尺测量电磁铁下端到M 的竖直距离作为小球下落的高度 |
D．手动敲击M 的同时按下秒表开始计时 |
（2）实验测得小球下落的高度H =1．980 m，10 个小球下落的总时间T =6．5 s．可求出重力加速度g =______
（结果保留两位有效数字）
（3）在不增加实验器材的情况下，请提出减小实验误差的两个办法．
（4）某同学考虑到电磁铁在每次断电后需要时间Δt 磁性才消失，因此，每个小球的实际下落时间与它的测量时间相差Δt，这导致实验误差较大。 为此，他分别取高度H1和H2，测量n个小球下落的总时间T1和T2．他是否可以利用这两组数据消除Δt 对实验结果的影响? 请推导说明．
