题目内容
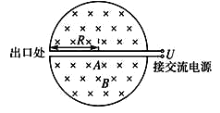
【题目】回旋加速器的工作原理如图所示，置于高真空中的D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生质量为m、电荷量为+q的粒子，在加速电压为U的加速电场中被加速。所加磁场的磁感应强度、加速电场的频率可调，磁场的磁感应强度最大值为Bm和加速电场频率的最大值fm。则下列说法正确的是
A. 粒子第n次和第n+1次半径之比总是
B. 粒子从静止开始加速到出口处所需的时间为
C. 若fm<
，则粒子获得的最大动能为
D. 若fm>
，则粒子获得的最大动能为
【答案】BCD
【解析】根据粒子在磁场中半径公式，及动能定理，则有： 
，与
与
解得： 
，故A错误；
设粒子到出口处被加速了n圈，解得：2nqU=
mv2； 
； 
；t=nT；解上四个方程得： 
，选项B正确；
加速电场的频率应该等于粒子在磁场中做圆周运动的频率，即： 
当磁感应强度为Bm时，加速电场的频率应该为： 
，粒子的动能：Ek=
mv2；当fBm≤fm时，粒子的最大动能由Bm决定，则： 
解得粒子获得的最大动能为
；当fBm≥fm时，粒子的最大动能由fm决定，则：vm=2πfmR，解得粒子获得的最大动能为Ekm=2π2mfm2R2 ；故CD正确．故选BCD．
练习册系列答案
名校课堂系列答案
相关题目
