题目内容
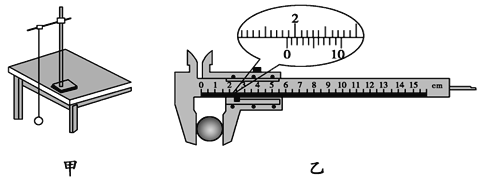
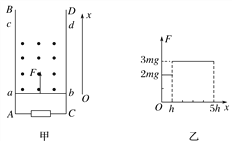
【题目】如图甲所示，一光滑的平行金属导轨ABCD竖直放置，AB、CD相距L，在A、C之间接一个阻值为R的电阻；在两导轨间的abcd矩形区域内有垂直导轨平面向外、高度为5h的有界匀强磁场，磁感应强度为B.一质量为m、电阻为r、长度也为L的导体棒放在磁场下边界ab上(与ab边重合).现用一个竖直向上的力F拉导体棒，使它由静止开始向上运动，导体棒刚要离开磁场时恰好做匀速直线运动，导体棒与导轨始终垂直且保持良好接触，导轨电阻不计.F随导体棒与初始位置的距离x变化的情况如图乙所示，下列说法正确的是
A. 导体棒离开磁场时速度大小为
B. 离开磁场时导体棒两端电压为
C. 导体棒经过磁场的过程中，通过电阻R的电荷量为
D. 导体棒经过磁场的过程中，电阻R产生焦耳热为
【答案】BD
【解析】A、设导体棒离开磁场时速度大小为v.此时导体棒受到的安培力大小为:
,由平衡条件得
，结合图像知 
,故A错误.
B、离开磁场时,由
得:
,导体棒两端电压为:
,所以B选项是正确的.
C、导体棒经过磁场的过程中,通过电阻R的电荷量为:
,故C错误.
D、导体棒经过磁场的过程中,设回路产生的总焦耳热为Q.根据功能关系可得:
而电阻R上分担的热量为
解得：
,所以D选项是正确的.
故选BD
解析：根据安培力与速度的关系式和平衡条件结合求导体棒离开磁场时的速度大小.根据
求通过电阻R的电荷量.根据欧姆定律求离开磁场时导体棒两端电压.根据功能关系求出电阻R产生的焦耳热.
练习册系列答案
发散思维新课堂系列答案
相关题目
