题目内容
【题目】在地面上有一破损的玻璃圆锥,其截面如图所示,经测量发现母线长AB=AC=R,∠CAB=75°,A恰好为圆心,弧CPB为以A为圆心的圆弧,某人将一单色光源放在BA延长线上的O点,其入射光线OD与母线AC的夹角为45°,该光线在弧面上的P点离开玻璃圆锥,其出射光线的方向与母线AB平行,已知玻璃对光的折射率为n=![]() ,sin75°=
,sin75°=![]() ,sin15°=
,sin15°=![]() 。求:
。求:
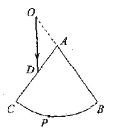
(i)从P点射出的光线与入射光线OP的夹角;
(ii)该光束在从P点穿出前在玻璃圆锥中传播的时间和在空气中由O到P传播的时间之比。
【答案】(i)300(ii)![]() 1
1
【解析】
(i)因出射的光线与母线AB平行,出射光线与入射光线OD方向的夹角即为OD与AB之间的夹角,根据几何知识可知,其夹角为
∠AOD=75°- 45°=30°
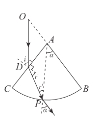
(ii)设AD=l,根据几何知识在△AOD中,
![]()
光在空气中传播的时间
![]()
![]() l
l
![]()
![]()
解得r=30°
在P点,根据折射定律,
![]()
根据几何关系知,
∠ADP=∠r+90°=120°
r’=180°-∠ADP-(75°-α)=α-15°
解得α=45°,r’=30°
在△ADP中
![]()
光在玻璃圆锥中传播的时间
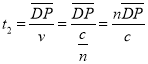
![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目