题目内容
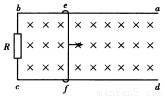
（20分）足够长的平行金属导轨ab、cd放置在水平面上，处在磁感应强度B=1.00T的竖直方向的匀强磁场中，导轨间连接阻值为R=0.30Ω的电阻，质量m=0.5kg的金属棒ef与bc紧贴在导轨上，处于两导轨间的长度L=0.40m、电阻r=0.10Ω，如图所示。在水平恒力F作用下金属棒ef由静止开始向右运动，其运动距离与时间的关系如下表所示。导轨与金属棒ef间的动摩擦因数为0.3，导轨电阻不计，g=10
求：
时间t(s) | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
运动距离x(m) | 0.0 | 0.6 | 2.0 | 4.3 | 6.8 | 9.3 | 11.8 | 14.3 |
（1）在4.0s时间内，通过金属棒截面的电荷量q；
（2）水平恒力F;
（3）庆丰同学在计算7.0s时间内，整个回路产生的焦耳热Q时，是这样计算的：
先算7.0s内的电荷量
再算电流
再用公式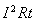
计算出焦耳热
请你简要分析这样做是否正确？认为正确的，请算出结果；认为错误的，请用自己的方法算出7.0s，整个回路产生的焦耳热Q。
【答案】
（1）6.8C? （2）2.5N? （3）12.7J
【解析】
试题分析：(1).金属棒产生的平均感应电动势
???? (1分)
平均电流
????? （1分）
电荷量
???? （2分）
(2).由表中数据可知3.0s以后棒ef做匀速直线运动
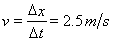??????? （2分）
F-f=BIL?????????? （2分）
由， E= BLv???????? （2分）
解得F=BIL+ f=2.5N???????? （3分）
(3)庆丰同学用电流的平均值计算焦耳热是错误的，?????? （2分）
根据能量转化和守恒定律有
（3分）
解得Q=12.7J??????????? （2分）
考点：本题考查电磁感应、能量守恒
练习册系列答案
相关题目
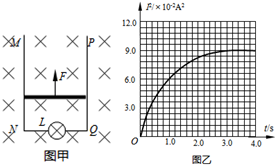如图甲所示，光滑且足够长的平行金属导轨MN、PQ固定在同一竖直面上，两导轨间距d=1m，电灯L的电阻R=4Ω，导轨上放一质量m=1kg、电阻r=1Ω的金属杆，长度与金属导轨等宽，与导轨接触良好，导轨的电阻不计，整个装置处于磁感应强度B=0.5T的匀强磁场中，磁场的方向垂直导轨平面向里．现用一拉力F沿竖直方向拉杆，使金属杆由静止开始向上运动，经3s上升了4m后开始做匀速运动．图乙所示为流过电灯L的电流平方随时间变化的I2-t图线，取g=10m/s2．求：
如图甲所示，光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上，两导轨间距为L=1m，定值电阻R1=4Ω，R2=2Ω，导轨上放一质量为m=1kg的金属杆，导轨和金属杆的电阻不计，整个装置处于磁感应强度为B=0.8T的匀强磁场中，磁场的方向垂直导轨平面向下，现用一拉力F沿水平方向拉杆，使金属杆由静止开始运动．图乙所示为通过R1中的电流平方随时间变化的I12-t图线，求：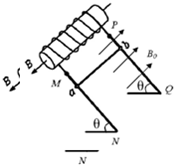
（2012?黄埔区模拟）如图所示，螺线管横截面积为S，线圈匝数为N，电阻为R1，管内有水平向左的变化磁场．螺线管与足够长的平行金属导轨MN、PQ相连并固定在同一平面内，与水平面的夹角为θ，两导轨间距为L．导轨电阻忽略不计．导轨处于垂直斜面向上、磁感应强度为B0的匀强磁场中．金属杆ab垂直导轨，杆与导轨接触良好，并可沿导轨无摩擦滑动．已知金属杆ab的质量为m，电阻为R2，重力加速度为g．忽略螺线管磁场对金属杆ab的影响、忽略空气阻力．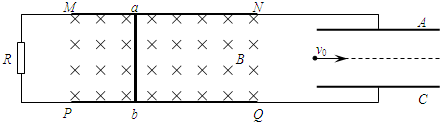
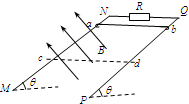如图所示，MN、PQ为足够长的平行金属导轨，间距L=0.50m，导轨平面与水平面间夹角θ=37°，N、Q间连接一个电阻R=5.0Ω，匀强磁场垂直于导轨平面向上，磁感应强度B=1.0T．将一根质量m=0.050kg的金属棒放在导轨的ab位置，金属棒的电阻为r=1.0Ω，导轨的电阻不计．现由静止释放金属棒，金属棒沿导轨向下运动过程中始终与导轨垂直，且与导轨接触良好．已知金属棒与导轨间的动摩擦因数μ=0.50，当金属棒滑行至cd处时速度大小开始保持不变，位置cd与ab之间的距离s=2.0m．已知g=10m/s2，sin37°=0.60，cos37°=0.80．求：