Question

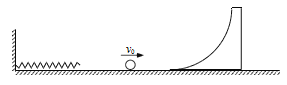
【题目】如图所示，足够长的光滑水平地面上有一个质量为m的小球，其右侧有一质量为M的斜劈，斜劈内侧为光滑圆弧。小球左侧有一轻弹簧，弹簧左侧固定于竖直墙壁上，右端自由。某时刻，小球获得一水平向右的初速度v0，求：

(1)若小球恰好不飞出斜劈，则斜劈内侧的圆弧半径R为多大；

(2)若小球从斜劈滚下后，能够继续向左运动，则弹簧具有的最大弹性势能Ep为多少；

(3)若整个过程中，弹簧仅被压缩一次，求满足此条件的的范围

Answer 1

【答案】(1) (2) (3)

【解析】

(1) 若小球恰好不飞出斜劈，则小球到达最高点时二者的速度恰好相等，选取向右为正方向，由动量守恒可得：

mv0=(m+M)v

又

联立解得

(2) 设小球第一次从斜劈B滑下离开时，小球和斜劈B的速度分别为v1和v2

以向右为正方向，由动量守恒可得

mv0=mv1+Mv2

由机械能守恒可得

联立解得小球速度为

斜劈B速度为

小球压缩弹簧的过程中系统的机械能守恒，小球的动能转化为弹簧的弹性势能，则：

(3) 设若整个过程中，弹簧仅被压缩一次，说明小球与斜劈分离后小球的速度方向必定向左，而且大小小于等于斜劈的速度大小，即：，即

可得：

则