题目内容
17. 如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为+q,速度为υ,MN的长度为L.
如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为+q,速度为υ,MN的长度为L.(1)若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度E0的最小值为多大?在电场强度为E0时,打到板上的粒子动能为多大?
(2)若在整个空间加一方向垂直纸面向里的匀强磁场,要使板右侧的MN连线上都有粒子打到,磁场的磁感应强度不能超过多少(用m、υ、q、L表示)?若满足此条件,放射源O向外发射出的所有带电粒子中有几分之几能打在板的左边?
分析 (1)要使y轴右侧所有运动粒子都能打在 MN板上,其临界条件为:沿y轴方向运动的粒子作类平抛运动,且落在M或N点.根据牛顿第二定律求出电场强度的最小值,根据动能定理求解打到板上粒子的动能.
(2)加匀强磁场后,粒子沿逆时针方向做匀速圆周运动,当轨迹以O′为圆心同时过M、N两点时,轨迹直径最小,得到粒子圆周运动的半径,由牛顿第二定律求出B的最大值.从O点向第四象限发射出的粒子均能打在MN板的左侧,占发射粒子总数的$\frac{1}{4}$.
解答 解:(1)由题意知,要使y轴右侧所有运动粒子都能打在MN板上,其临界条件为:沿y轴方向运动的粒子作类平抛运动,且落在M或N点.
则M O′=$\frac{1}{2}L=vt$…①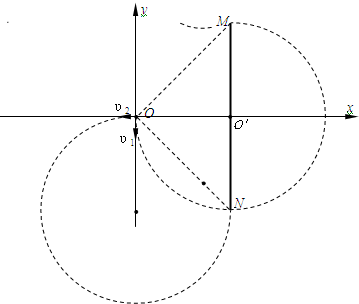
加速度a=$\frac{q{E}_{0}}{m}$…②
OO′=$\frac{1}{2}L=\frac{1}{2}a{t}^{2}$…③
解①②③式得
E0=$\frac{4m{v}^{2}}{qL}$…④
由动能定理知
qE0×$\frac{1}{2}L$=${E}_{k}-\frac{1}{2}m{v}^{2}$…⑤
解④⑤式得:
Ek=$\frac{5}{2}m{v}^{2}$
(2)由题意知,要使板右侧的MN连线上都有粒子打到,粒子轨迹直径的最小值为MN板的长度L.
R0=$\frac{1}{2}L$=$\frac{mv}{q{B}_{0}}$
B0=$\frac{2mv}{qL}$
放射源O发射出的粒子中,打在MN板上的粒子的临界径迹如图所示.
因为OM=ON,且OM⊥ON
所以OO1⊥OO2
则υ1⊥υ2
可知放射源O放射出的所有粒子中只有$\frac{1}{4}$打在MN板的左侧.
答:(1)电场强度E0的最小值为$\frac{4m{v}^{2}}{qL}$;在电场强度为E0时,打到板上的粒子动能为$\frac{5}{2}m{v}^{2}$;
(2)放射源O放射出的所有粒子中只有$\frac{1}{4}$打在MN板的左侧.
点评 本题中粒子在电场中做类平抛运动时运用运动的合成和分解法研究,在磁场中要通过画出轨迹,确定临界条件求解磁感应强度.

 阅读快车系列答案
阅读快车系列答案| A. | 车在最高点时人处于倒立状态,全靠保险带拉住,没有保险带人就会掉下来 | |
| B. | 人在最高点时对座位仍可能产生压力 | |
| C. | 人在最低点时处于超重状态 | |
| D. | 人在最高点时处于超重状态 |
| A. | 在伽利略之前的学者们总是通过思辩性的论战决定谁是谁非,是他首先采用了以实验检验猜想和假设的科学方法 | |
| B. | 伽利略斜面实验是将可靠的事实和抽象思维结合起来,能更深刻地反映自然规律 | |
| C. | 探究加速度与力、质量三个物理量之间的定量关系,可以在质量一定的情况下,探究物体的加速度与力的关系;再在物体受力一定的情况下,探究物体的加速度与质量的关系.最后归纳出加速度与力、质量之间的关系.这是物理学中常用的控制变量的研究方法 | |
| D. | 在公式I=$\frac{U}{R}$电压U和电流I具有因果关系、公式E=n$\frac{△Φ}{△t}$中△Φ和E具有因果关系,同理在a=$\frac{△V}{△t}$中△V和a具有因果关系 |
 如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )
如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )| A. | 该电场是匀强电场 | B. | 电子在A、B两点的速度vA<vB | ||
| C. | A、B两点的电势φA>φB | D. | 电子在A、B两点的电势能EpA<EpB |

| A. | 电压表的示数为22V | B. | R处出现火情时电压表示数增大 | ||
| C. | R处出现火情时电流表示数增大 | D. | R处出现火情时R0消耗的功率增大 |
| A. | 96 240 | B. | 96 241 | C. | 95 240 | D. | 95 241 |
 如图所示电路,已知灯泡a、R1、R2、R3的电阻和电源的内阻为R,线圈L的直流电阻为零,现灯泡正常发光.由于电路出现故障,灯泡亮度发生变化,以下说法正确的是( )
如图所示电路,已知灯泡a、R1、R2、R3的电阻和电源的内阻为R,线圈L的直流电阻为零,现灯泡正常发光.由于电路出现故障,灯泡亮度发生变化,以下说法正确的是( )| A. | 如果R2或R3短路,灯泡亮度将突然增加,电源输出功率最终减小 | |
| B. | 如果R2或R3短路,灯泡亮度将突然减弱,电源效率最终减小 | |
| C. | 如果R1短路,灯泡亮度逐渐增加,电源输出功率最终增大 | |
| D. | 如果R1短路,灯泡亮度逐渐减弱,路端电压最终减小 |
 在足够长的水平光滑直导轨上,静止放着三个质量均为m=1kg的小球A、B、C,现让A球以v0=2m/s的速度正对着B球运动,A、B两球碰撞后粘在一起,两球继续向右运动并与C球发生正碰,C球的最终速度vC=1m/s.求:
在足够长的水平光滑直导轨上,静止放着三个质量均为m=1kg的小球A、B、C,现让A球以v0=2m/s的速度正对着B球运动,A、B两球碰撞后粘在一起,两球继续向右运动并与C球发生正碰,C球的最终速度vC=1m/s.求: 如图所示,O为一水平轴.细绳上端固定于O轴,下端系一质量m=1.0kg的小球B,小球B与平台的边缘处接触但无压力,且处于静止状态.一个质量为M=3.0kg的小球A以某一速度v0沿光滑平台自左向右运动与小球B发生正碰,碰后小球B在绳的约束下做圆周运动,经最高点时,绳上的拉力T恰好等于摆球的重力,而小球A落在水平地面的位置距平台边缘的水平距离S=0.8m.已知细绳长为l=0.6m,平台高h=0.80m,重力加速度g=10m/s2,不计空气阻力.求:
如图所示,O为一水平轴.细绳上端固定于O轴,下端系一质量m=1.0kg的小球B,小球B与平台的边缘处接触但无压力,且处于静止状态.一个质量为M=3.0kg的小球A以某一速度v0沿光滑平台自左向右运动与小球B发生正碰,碰后小球B在绳的约束下做圆周运动,经最高点时,绳上的拉力T恰好等于摆球的重力,而小球A落在水平地面的位置距平台边缘的水平距离S=0.8m.已知细绳长为l=0.6m,平台高h=0.80m,重力加速度g=10m/s2,不计空气阻力.求: