题目内容
17.有一根很细的均匀空心金属管线重约1N、长约50cm、电阻约为30-40Ω,现需测定它的内径d,已知这种金属的电阻率为ρ.实验室中可以提供下列器材:A.厘米刻度尺;
B.毫米刻度尺;
C.螺旋测微器;
D.电流表(300mA,约10Ω);
E.电流表(3A,约0.1Ω);
F.电压表(3V,6KΩ);
G.滑动变阻器(200Ω,0.5A);
H.滑动变阻器(5Ω,2A);
I.蓄电池(6V,0.05Ω);
J.开关一个及带夹的异线若干.
请设计一个实验方案,回答以下问题:
①实验中应测物理量的名称及符号是金属管线的长度L、外径D,加在管线两端的电压U,通过管线的电流强度为I;
②应选用的实验器材有(只填字母代号):B、C、D、F、H、I、J.
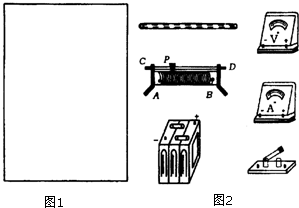
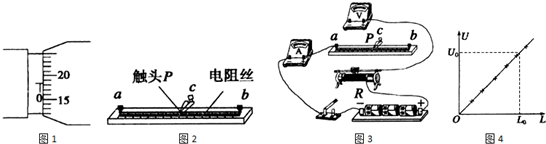
③在方框中(图1)画出实验电路图并将图2中所示仪器连成实际测量电路;
④用测得的物理量和已知的物理常数推导出计算金属管线内径d的表达式.
分析 ①本实验通过欧姆定律结合电阻定律测量金属杆的内径,根据实验的原理确定需要测量的物理量;
②根据电路最大电流选择电流表,为方便实验操作应选最大阻值较小的滑动变阻器,根据实验原理与实验需要测量的量选择实验器材;
③根据题意确定电流表与滑动变阻器的接法,然后作出实验电路图,根据实验电路图连接实物电路图;
④应用欧姆定律求出电阻,应用电阻定律与面积公式求出内径表达式.
解答 解:①该实验需要测量空心金属管的内径,通过欧姆定律测出电阻的大小,结合电阻定律测出横截面积,从而根据外径求出内径的大小.故所需测量的物理量为金属管的长度L、金属管的外径D、加在管两端的电压U、通过管的电流强度I.
②测长度需要毫米刻度尺B,测外径需要螺旋测微器C,需要电压表F,电源I及导线J,
电压表量程为3V,通过金属管的最大电流约为:I=$\frac{U}{R}$=$\frac{3V}{30Ω}$=0.1A=100mA,电流表应选择D;
为方便实验操作,滑动变阻器应选择H,因此需要的实验器材有:B、C、D、F、H、I、J;
③待测电阻阻值约为30-40Ω,电流表内阻约为10Ω,电压表内阻约为6kΩ,电压表内阻远大于待测电阻阻值,电流表采用外接法,
滑动变阻器最大阻值为5Ω,远小于待测电阻阻值,为测多组实验数据,滑动变阻器应采用分压接法,电路图如图所示,
根据电路图连接实物电路图,实物电路图如图所示;
④金属管线的电阻:R=$\frac{U}{I}$,
由电阻定律可知:R=ρ$\frac{L}{S}$,
整理得:S=$\frac{ρLI}{U}$,
金属管线的横截面积:S=π$(\frac{D}{2})^{2}$-π$(\frac{d}{2})^{2}$,
解得:d=$\sqrt{{D}^{2}-\frac{4ρLI}{πU}}$.
故答案为:①金属管线的长度L、外径D,加在管线两端的电压U,通过管线的电流强度为I;
②B、C、D、F、H、I、J;③电路图与实物电路图如图所示;④d=$\sqrt{{D}^{2}-\frac{4ρLI}{πU}}$.
点评 解决本题的关键知道实验的原理,操作步骤,以及知道实验误差形成的原因.掌握滑动变阻器分压、限流式接法的区别,以及电流表内外接的区别.

| A. | 质量 | B. | 机械能 | C. | 向心力 | D. | 加速度 |
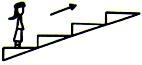 为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上梯时,它会先慢慢加速,再匀速运转,一顾客乘扶梯上搂,恰好经历了这两个过程,如图所示.则在加速过程中,下列说法中正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上梯时,它会先慢慢加速,再匀速运转,一顾客乘扶梯上搂,恰好经历了这两个过程,如图所示.则在加速过程中,下列说法中正确的是( )| A. | 顾客受到三个力的作用 | B. | 顾客处于失重状态 | ||
| C. | 扶梯对顾客没有摩擦力的作用 | D. | 顾客对扶梯的压力等于顾客的重量 |
| A. |  | B. |  | C. |  | D. |  |
 在“利用自由落体运动验证机械能守恒定律”的实验中,若打点计时器所接交变电流的频率为50Hz,得到的甲、乙两条实验纸带(如图所示)中应选甲纸带更好.若已测得点2到点4间的距离为s1,点0到点3间的距离为s2,打点周期为T,要验证重物从开始下落到打点计时器打下点3这段时间内机械能守恒,则s1、s2和T应满足的关系为:T=$\frac{{s}_{1}\sqrt{2g{s}_{2}}}{4g{s}_{2}}$.
在“利用自由落体运动验证机械能守恒定律”的实验中,若打点计时器所接交变电流的频率为50Hz,得到的甲、乙两条实验纸带(如图所示)中应选甲纸带更好.若已测得点2到点4间的距离为s1,点0到点3间的距离为s2,打点周期为T,要验证重物从开始下落到打点计时器打下点3这段时间内机械能守恒,则s1、s2和T应满足的关系为:T=$\frac{{s}_{1}\sqrt{2g{s}_{2}}}{4g{s}_{2}}$.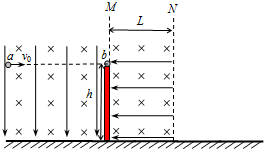 如图所示,地面上方竖直界面N左侧空间存在着水平的、垂直纸面向里的匀强磁场,磁感应强度B=2.0T.与N平行的竖直界面M左侧存在竖直向下的匀强电场,电场强度E1=100N/C.在界面M与N之间还同时存在着水平向左的匀强电场,电场强度E2=100N/C.在紧靠界面M处有一个固定在水平地面上的竖直绝缘支架,支架上表面光滑,支架上放有质量m2=1.8×10-4kg的带正电的小物体b(可视为质点),电荷量q2=1.0×10-5 C.一个质量为m1=1.8×10-4kg,电荷量为q1=3.0×10-5 C的带负电小物体(可视为质点)a以水平速度v0射入场区,沿直线运动并与小物体b相碰,a、b两个小物体碰后粘合在一起成小物体c,进入界面M右侧的场区,并从场区右边界N射出,落到地面上的Q点(图中未画出).已知支架顶端距地面的高度h=1.0m,M和N两个界面的距离L=0.10m,g取10m/s2.求:
如图所示,地面上方竖直界面N左侧空间存在着水平的、垂直纸面向里的匀强磁场,磁感应强度B=2.0T.与N平行的竖直界面M左侧存在竖直向下的匀强电场,电场强度E1=100N/C.在界面M与N之间还同时存在着水平向左的匀强电场,电场强度E2=100N/C.在紧靠界面M处有一个固定在水平地面上的竖直绝缘支架,支架上表面光滑,支架上放有质量m2=1.8×10-4kg的带正电的小物体b(可视为质点),电荷量q2=1.0×10-5 C.一个质量为m1=1.8×10-4kg,电荷量为q1=3.0×10-5 C的带负电小物体(可视为质点)a以水平速度v0射入场区,沿直线运动并与小物体b相碰,a、b两个小物体碰后粘合在一起成小物体c,进入界面M右侧的场区,并从场区右边界N射出,落到地面上的Q点(图中未画出).已知支架顶端距地面的高度h=1.0m,M和N两个界面的距离L=0.10m,g取10m/s2.求: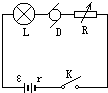 如图所示电路,电源电动势ε=14V,内阻r=1Ω,电灯L为:“2V,4W”,电动机D的内阻R’=0.5Ω,当可变电阻的阻值为R=1Ω时,电灯和电动机都正常工作,则电动机的额定电压为8V,电动机输出的机械功率为14W,全电路工作1min放出的焦耳热为840J.
如图所示电路,电源电动势ε=14V,内阻r=1Ω,电灯L为:“2V,4W”,电动机D的内阻R’=0.5Ω,当可变电阻的阻值为R=1Ω时,电灯和电动机都正常工作,则电动机的额定电压为8V,电动机输出的机械功率为14W,全电路工作1min放出的焦耳热为840J.