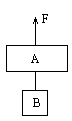
题目内容
如图9所示,两个质点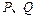 在光滑的水平面上分别以一定的速度同时向右运动,此时分别作用水平向左的力
在光滑的水平面上分别以一定的速度同时向右运动,此时分别作用水平向左的力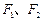 ,其中
,其中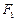 的大小不变,
的大小不变,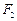 大小由零逐渐增大,它们恰好同时向右运动最远,且位移大小相等,在此过程中,两质点的瞬时速度
大小由零逐渐增大,它们恰好同时向右运动最远,且位移大小相等,在此过程中,两质点的瞬时速度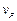 与
与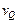 的关系应该是 ( )
的关系应该是 ( )
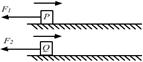
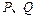 在光滑的水平面上分别以一定的速度同时向右运动,此时分别作用水平向左的力
在光滑的水平面上分别以一定的速度同时向右运动,此时分别作用水平向左的力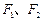 ,其中
,其中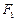 的大小不变,
的大小不变,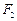 大小由零逐渐增大,它们恰好同时向右运动最远,且位移大小相等,在此过程中,两质点的瞬时速度
大小由零逐渐增大,它们恰好同时向右运动最远,且位移大小相等,在此过程中,两质点的瞬时速度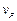 与
与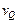 的关系应该是 ( )
的关系应该是 ( )A.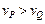 . . | B.先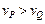 ,后 ,后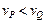 ,最后 ,最后 . . |
C.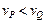 . . | D.先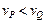 ,后 ,后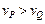 ,最后 ,最后 . . |

B
这是用解析法很难下手的题目,但若能利用题设条件,分析并画好两个质点的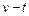 图像,就能很快找到答案.如图所示,由于
图像,就能很快找到答案.如图所示,由于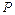 受力
受力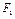 的大小不变,在
的大小不变,在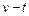 图像中画出
图像中画出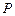 做匀减速运动的
做匀减速运动的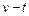 图像,由于
图像,由于 受力
受力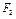 的大小逐渐增大,
的大小逐渐增大, 做加速度不断增大的减速运动,其
做加速度不断增大的减速运动,其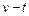 图像是一条曲线.在
图像是一条曲线.在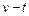 图像上,任一点的切线的斜率数值上等于在该时刻的加速度,由于
图像上,任一点的切线的斜率数值上等于在该时刻的加速度,由于 的加速度由零不断增大,画出曲线切线斜率的绝对值也应从零开始不断增大,即曲线的切线应从水平状态开始不断变陡,那么只有向右边凸出的下降的曲线才能满足这样的条件,又因
的加速度由零不断增大,画出曲线切线斜率的绝对值也应从零开始不断增大,即曲线的切线应从水平状态开始不断变陡,那么只有向右边凸出的下降的曲线才能满足这样的条件,又因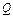 与
与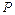 的运动时间相等,所以曲线的终点也应在
的运动时间相等,所以曲线的终点也应在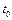 ,
,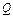 与
与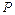 的运动位移大小相等,所以曲线包围的面积应等于
的运动位移大小相等,所以曲线包围的面积应等于 的面积,根据这些要求,曲线的起点、即质点
的面积,根据这些要求,曲线的起点、即质点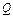 的初速度
的初速度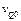 必定小于
必定小于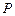 点的初速度
点的初速度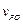 ,且两条
,且两条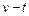 图像必定会相交,如图中的实线所示,图中的两条虚线表示的质点
图像必定会相交,如图中的实线所示,图中的两条虚线表示的质点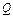 的
的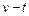 图像都不满足题设条件(
图像都不满足题设条件(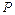 与
与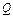 的位移大小相等),所以B对.
的位移大小相等),所以B对.

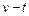 图像,就能很快找到答案.如图所示,由于
图像,就能很快找到答案.如图所示,由于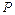 受力
受力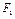 的大小不变,在
的大小不变,在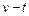 图像中画出
图像中画出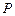 做匀减速运动的
做匀减速运动的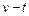 图像,由于
图像,由于 受力
受力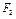 的大小逐渐增大,
的大小逐渐增大, 做加速度不断增大的减速运动,其
做加速度不断增大的减速运动,其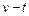 图像是一条曲线.在
图像是一条曲线.在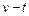 图像上,任一点的切线的斜率数值上等于在该时刻的加速度,由于
图像上,任一点的切线的斜率数值上等于在该时刻的加速度,由于 的加速度由零不断增大,画出曲线切线斜率的绝对值也应从零开始不断增大,即曲线的切线应从水平状态开始不断变陡,那么只有向右边凸出的下降的曲线才能满足这样的条件,又因
的加速度由零不断增大,画出曲线切线斜率的绝对值也应从零开始不断增大,即曲线的切线应从水平状态开始不断变陡,那么只有向右边凸出的下降的曲线才能满足这样的条件,又因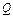 与
与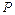 的运动时间相等,所以曲线的终点也应在
的运动时间相等,所以曲线的终点也应在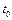 ,
,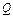 与
与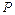 的运动位移大小相等,所以曲线包围的面积应等于
的运动位移大小相等,所以曲线包围的面积应等于 的面积,根据这些要求,曲线的起点、即质点
的面积,根据这些要求,曲线的起点、即质点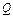 的初速度
的初速度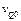 必定小于
必定小于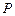 点的初速度
点的初速度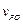 ,且两条
,且两条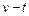 图像必定会相交,如图中的实线所示,图中的两条虚线表示的质点
图像必定会相交,如图中的实线所示,图中的两条虚线表示的质点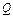 的
的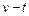 图像都不满足题设条件(
图像都不满足题设条件(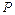 与
与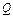 的位移大小相等),所以B对.
的位移大小相等),所以B对.

练习册系列答案
相关题目
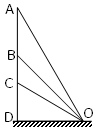

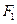 作用(m可视为质点),在MN的右方除受
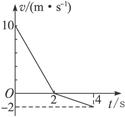
作用(m可视为质点),在MN的右方除受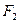 作用,现设小球由A点从静止开始运动,如图(a)所示,小球运动的
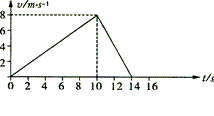
作用,现设小球由A点从静止开始运动,如图(a)所示,小球运动的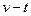 图象如图(b)所示,由图可知下列说法正确的是( )
图象如图(b)所示,由图可知下列说法正确的是( )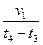
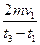
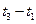
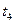 这段时间最大位移为
这段时间最大位移为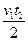 ,小球最终能回到A点
,小球最终能回到A点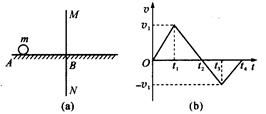
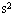 )
)