题目内容
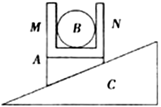
如图所示,AO、BO、BO是竖直面内三根固定的光滑细杆,与水平面的夹角依次是60°、45°、30°,直线AD与地面垂直。每根杆上都套着一个小滑环(图中未画出),三个滑环分别从A、B、C 处释放(初速为0),用t1、t2、t3依次表示滑环到达O所用的时间,则( )
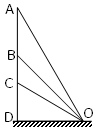
A.t1 < t2 < t3 B.t1 > t2 > t3
C.t1 = t3 > t2 D.t3 = t1 = t2

A.t1 < t2 < t3 B.t1 > t2 > t3
C.t1 = t3 > t2 D.t3 = t1 = t2
C
设OD=d,任意一斜面的倾角为α,则由牛顿第二定律得到滑环的加速度为 a=gsinα,滑环从斜面的顶点滑到D的位移为 x=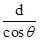 .由x=
.由x= at2得,t=
at2得,t=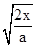 =
=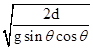 =
= ,由数学知识得知,sin(2×60°)=sin(2×30°),sin(2×45°)=1最大,则知t1=t3>t2.故C正确.
,由数学知识得知,sin(2×60°)=sin(2×30°),sin(2×45°)=1最大,则知t1=t3>t2.故C正确.
本题是牛顿第二定律和运动学公式的综合应用,关键要抓住三个过程相同的量表示位移和加速度.
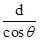 .由x=
.由x= at2得,t=
at2得,t=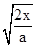 =
=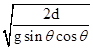 =
= ,由数学知识得知,sin(2×60°)=sin(2×30°),sin(2×45°)=1最大,则知t1=t3>t2.故C正确.
,由数学知识得知,sin(2×60°)=sin(2×30°),sin(2×45°)=1最大,则知t1=t3>t2.故C正确.本题是牛顿第二定律和运动学公式的综合应用,关键要抓住三个过程相同的量表示位移和加速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
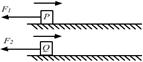
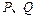 在光滑的水平面上分别以一定的速度同时向右运动,此时分别作用水平向左的力
在光滑的水平面上分别以一定的速度同时向右运动,此时分别作用水平向左的力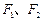 ,其中
,其中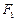 的大小不变,
的大小不变,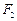 大小由零逐渐增大,它们恰好同时向右运动最远,且位移大小相等,在此过程中,两质点的瞬时速度
大小由零逐渐增大,它们恰好同时向右运动最远,且位移大小相等,在此过程中,两质点的瞬时速度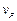 与
与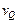 的关系应该是 ( )
的关系应该是 ( )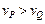 .
.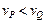 ,最后
,最后 .
.

 则该质点一定不能处于平衡状态
则该质点一定不能处于平衡状态