题目内容
2.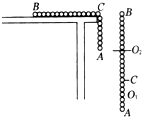 如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )
如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )| A. | v=$\frac{1}{3}$gL | B. | $\frac{{\sqrt{3}}}{3}$gL | C. | $\sqrt{3}$gL | D. | v=$\frac{2}{3}\sqrt{2gL}$ |
分析 在运动的过程中,对整个系统而言,机械能守恒.抓住系统重力势能的减小量等于动能的增加量,分别求出离开桌面时的速度.
解答 解:铁链释放之后,到离开桌面到落地的过程,由于桌面无摩擦,整个链条的机械能守恒.取桌面为零势能面,整个软绳的质量为m.
根据机械能守恒定律得:
-$\frac{1}{3}$mg•$\frac{L}{6}$=$\frac{1}{2}$mv2-mg×(0.5L)
解得:v=$\frac{2}{3}\sqrt{2gL}$
故选:D.
点评 本题为机械能守恒定律应用的问题,要注意正确设定零势能面;本题中也可以选取地面为零势能面

练习册系列答案
相关题目
12. 如图所示,一小滑块沿足够长的斜面以初速度v向上做匀减速直线运动,依次经A,B,C,D 到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经C时的速度为vc,则( )
如图所示,一小滑块沿足够长的斜面以初速度v向上做匀减速直线运动,依次经A,B,C,D 到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经C时的速度为vc,则( )
 如图所示,一小滑块沿足够长的斜面以初速度v向上做匀减速直线运动,依次经A,B,C,D 到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经C时的速度为vc,则( )
如图所示,一小滑块沿足够长的斜面以初速度v向上做匀减速直线运动,依次经A,B,C,D 到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经C时的速度为vc,则( )| A. | vc=6m/s | |
| B. | 从D到E所用时间为2s | |
| C. | DE=3m | |
| D. | 滑块上滑过程中加速度的大小为0.5m/s2 |
10.关于自由落体运动的说法正确的是( )
| A. | 竖直方向的运动就是自由落体运动 | |
| B. | 初速度为零的匀加速直线运动就是自由落体运动 | |
| C. | 自由落体运动的方向为竖直向下 | |
| D. | 物体只在重力作用下的运动为自由落体运动 |
 消防训练,要求消防队沿固定在高处的竖直绳子由静止开始下滑然后安全着地.在绳子上端装有测力传感器,测出某消防队员下滑过程中悬点对绳子的作用力变化情况如图示,测得该消防队员质量为50kg,绳子质量10kg,取g=l0m/s2,求
消防训练,要求消防队沿固定在高处的竖直绳子由静止开始下滑然后安全着地.在绳子上端装有测力传感器,测出某消防队员下滑过程中悬点对绳子的作用力变化情况如图示,测得该消防队员质量为50kg,绳子质量10kg,取g=l0m/s2,求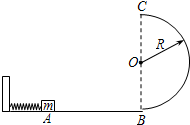 如图所示,光滑水平面AB与竖直面内的半圆形轨道在B点相接,轨道半径为R.一个质量为m的物体(可视为质点)将轻质弹簧压缩至A点后由静止释放,在弹力作用下物体水平向右运动至某一速度时脱离弹簧,当它经过B点进入轨道瞬间对轨道的压力为其重力的8倍,之后向上运动到达C点时对轨道的压力大小为0.5mg.求:
如图所示,光滑水平面AB与竖直面内的半圆形轨道在B点相接,轨道半径为R.一个质量为m的物体(可视为质点)将轻质弹簧压缩至A点后由静止释放,在弹力作用下物体水平向右运动至某一速度时脱离弹簧,当它经过B点进入轨道瞬间对轨道的压力为其重力的8倍,之后向上运动到达C点时对轨道的压力大小为0.5mg.求: