题目内容
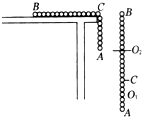
12. 如图所示,一小滑块沿足够长的斜面以初速度v向上做匀减速直线运动,依次经A,B,C,D 到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经C时的速度为vc,则( )
如图所示,一小滑块沿足够长的斜面以初速度v向上做匀减速直线运动,依次经A,B,C,D 到达最高点E,已知AB=BD=6m,BC=1m,滑块从A到C和从C到D所用的时间都是2s.设滑块经C时的速度为vc,则( )| A. | vc=6m/s | |
| B. | 从D到E所用时间为2s | |
| C. | DE=3m | |
| D. | 滑块上滑过程中加速度的大小为0.5m/s2 |
分析 根据匀变速直线运动连续相等时间内的位移之差是一恒量气促滑块上滑的加速度.根据某段时间内的平均速度等于中间时刻的瞬时速度求出C点的瞬时速度.根据速度位移公式求出CE的距离,从而得出DE的距离.根据速度时间公式求出CE的时间,从而得出DE段的时间.
解答 解:A、C点是AD段的中间时刻,所以C点的速度等于AD段的平均速度,则${v}_{C}=\frac{{x}_{AD}}{2t}=\frac{12}{4}m/s=3m/s$.故A错误.
B、因为xAC=7m,xCD=5m,根据△x=at2得,a=$\frac{△x}{{t}^{2}}=\frac{-2}{4}m/{s}^{2}=-0.5m/{s}^{2}$.、根据匀变速直线运动的速度位移公式得,${x}_{CE}=\frac{0-{{v}_{c}}^{2}}{2a}=\frac{-9}{-1}m=9m$,则DE=9-(6-1)m=4m.从D点到E点的时间t=$\frac{0-{v}_{c}}{a}=\frac{3}{-0.5}s=6s$,则D到E的时间为4s.故D正确.BC错误
故选:D.
点评 本题考查匀变速直线运动的规律应用;解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用.

练习册系列答案
相关题目
2.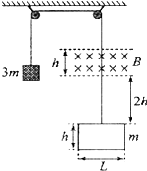 如图所示,质量为3m的重物与一质量为m的导线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知导线框电阻为R,横边边长为L.有一垂直纸面向里的匀强磁场,磁感应强度为B,磁场上下边界的距离、导线框竖直边长均为h.初始时刻,磁场的下边缘和导线框上边缘的高度差为2h,将重物从静止开始释放,导线框加速进入磁场,穿出磁场前已经做匀速直线运动,滑轮质量、摩擦阻力均不计,重力加速度为g.则下列说法中正确的是( )
如图所示,质量为3m的重物与一质量为m的导线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知导线框电阻为R,横边边长为L.有一垂直纸面向里的匀强磁场,磁感应强度为B,磁场上下边界的距离、导线框竖直边长均为h.初始时刻,磁场的下边缘和导线框上边缘的高度差为2h,将重物从静止开始释放,导线框加速进入磁场,穿出磁场前已经做匀速直线运动,滑轮质量、摩擦阻力均不计,重力加速度为g.则下列说法中正确的是( )
 如图所示,质量为3m的重物与一质量为m的导线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知导线框电阻为R,横边边长为L.有一垂直纸面向里的匀强磁场,磁感应强度为B,磁场上下边界的距离、导线框竖直边长均为h.初始时刻,磁场的下边缘和导线框上边缘的高度差为2h,将重物从静止开始释放,导线框加速进入磁场,穿出磁场前已经做匀速直线运动,滑轮质量、摩擦阻力均不计,重力加速度为g.则下列说法中正确的是( )
如图所示,质量为3m的重物与一质量为m的导线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知导线框电阻为R,横边边长为L.有一垂直纸面向里的匀强磁场,磁感应强度为B,磁场上下边界的距离、导线框竖直边长均为h.初始时刻,磁场的下边缘和导线框上边缘的高度差为2h,将重物从静止开始释放,导线框加速进入磁场,穿出磁场前已经做匀速直线运动,滑轮质量、摩擦阻力均不计,重力加速度为g.则下列说法中正确的是( )| A. | 导线框进入磁场时的速度为$\sqrt{gh}$ | |
| B. | 导线框进入磁场后,若某一时刻的速度为v,则加速度为a=$\frac{1}{2}$g-$\frac{{B}^{2}{L}^{2}v}{4mR}$ | |
| C. | 导线框穿出磁场时的速度为 $\frac{mgR}{{B}^{2}{L}^{2}}$ | |
| D. | 导线框通过磁场的过程中产生的热量Q=8mgh-$\frac{8{m}^{3}{g}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$ |
3.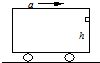 如图,以速度v匀速行驶的车厢,突然以加速度a作匀加速运动,小球恰从车厢内高度为h的架子上落下,则落在车厢地板上的点距架子的水平距离为( )
如图,以速度v匀速行驶的车厢,突然以加速度a作匀加速运动,小球恰从车厢内高度为h的架子上落下,则落在车厢地板上的点距架子的水平距离为( )
 如图,以速度v匀速行驶的车厢,突然以加速度a作匀加速运动,小球恰从车厢内高度为h的架子上落下,则落在车厢地板上的点距架子的水平距离为( )
如图,以速度v匀速行驶的车厢,突然以加速度a作匀加速运动,小球恰从车厢内高度为h的架子上落下,则落在车厢地板上的点距架子的水平距离为( )| A. | 0 | B. | $\frac{ah}{g}$ | C. | v$\sqrt{\frac{2h}{g}}$ | D. | v$\sqrt{\frac{2v}{a}}$ |
7.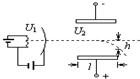 如图是一个说明示波管工作的原理图,电子经加速电场(加速电压为U1)加速后垂直进入偏转电场,离开偏转电场时偏转量是h,两平行板间的距离为d,电压为U2,板长为l,每单位电压引起的偏移$\frac{h}{U_2}$,叫做示波管的灵敏度,为了提高灵敏度,可采用下列哪些方法( )
如图是一个说明示波管工作的原理图,电子经加速电场(加速电压为U1)加速后垂直进入偏转电场,离开偏转电场时偏转量是h,两平行板间的距离为d,电压为U2,板长为l,每单位电压引起的偏移$\frac{h}{U_2}$,叫做示波管的灵敏度,为了提高灵敏度,可采用下列哪些方法( )
 如图是一个说明示波管工作的原理图,电子经加速电场(加速电压为U1)加速后垂直进入偏转电场,离开偏转电场时偏转量是h,两平行板间的距离为d,电压为U2,板长为l,每单位电压引起的偏移$\frac{h}{U_2}$,叫做示波管的灵敏度,为了提高灵敏度,可采用下列哪些方法( )
如图是一个说明示波管工作的原理图,电子经加速电场(加速电压为U1)加速后垂直进入偏转电场,离开偏转电场时偏转量是h,两平行板间的距离为d,电压为U2,板长为l,每单位电压引起的偏移$\frac{h}{U_2}$,叫做示波管的灵敏度,为了提高灵敏度,可采用下列哪些方法( )| A. | 增大U1 | B. | 减小U2 | C. | 增大l | D. | 减小d |
17.某星球的密度跟地球的密度相同,一物体在该星球表面所受重力是它在地球表面所受重力的3倍,则该星球的质量是地球质量的( )倍 (球的体积与球的半径的立方成正比)
| A. | $\frac{1}{3}$ | B. | 3 | C. | 9 | D. | 27 |
1.图是α粒子散射实验的结果示意图,说法正确的是( )
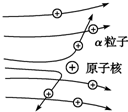

| A. | 汤姆孙的原子模型能很好解释α粒子散射实验的结果 | |
| B. | 该实验证明了原子的全部正电荷和几乎全部质量都集中在一个很小的核里 | |
| C. | 用该实验测算出,原子核直径的数量级为10-15 m | |
| D. | 该实验说明了原子中的电子只能在某些轨道上运动 |
2. 如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )
如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )
 如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )
如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )| A. | v=$\frac{1}{3}$gL | B. | $\frac{{\sqrt{3}}}{3}$gL | C. | $\sqrt{3}$gL | D. | v=$\frac{2}{3}\sqrt{2gL}$ |
 用伏安法测电池电动势E以及内阻r.按照实验值作出U-I图线,由此图线求得该电池电动势E=2.96V,电源内阻r=0.738Ω.(取3位有效数字)
用伏安法测电池电动势E以及内阻r.按照实验值作出U-I图线,由此图线求得该电池电动势E=2.96V,电源内阻r=0.738Ω.(取3位有效数字)