题目内容
14. 消防训练,要求消防队沿固定在高处的竖直绳子由静止开始下滑然后安全着地.在绳子上端装有测力传感器,测出某消防队员下滑过程中悬点对绳子的作用力变化情况如图示,测得该消防队员质量为50kg,绳子质量10kg,取g=l0m/s2,求
消防训练,要求消防队沿固定在高处的竖直绳子由静止开始下滑然后安全着地.在绳子上端装有测力传感器,测出某消防队员下滑过程中悬点对绳子的作用力变化情况如图示,测得该消防队员质量为50kg,绳子质量10kg,取g=l0m/s2,求(1)消防队员落地时的速度.
(2)下滑过程中,消防队员克服摩擦力做的功.
分析 (1)根据牛顿运动定律知加速度,根据速度时间关系知速度;
(2)根据位移时间关系求解下落高度,对全过程应用动能定理知摩擦力做功.
解答 解:(1)0-6秒内,加速下滑,Mg-(F1-mg)=ma1
解得:a1=1m/s2
2-8秒内,减速下滑,Mg-(F2-mg)=ma2
解得:${a_2}=-2m/{s^2}$
则v=a1t1+a2t2=2m/s
(2)0-6秒内,消防队员下落的高度为${h_1}=\frac{1}{2}{a_1}t_1^2=18m$
6-8秒内,消防队员下落的高度为${h_2}=\frac{1}{2}(2{a_1}{t_1}+{a_2}t_2^{\;}){t_2}=8m$
由动能定理得:$Mg({h_1}+{h_2})-{W_f}=\frac{1}{2}M{v^2}$
解得:${W_f}=Mg({h_1}+{h_2})-\frac{1}{2}M{v^2}$=12900J
即消防队员克服摩擦力做的功12900J
答:(1)消防队员落地时的速度为2m/s.
(2)下滑过程中,消防队员克服摩擦力做的功为12900J.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系前后的桥梁.对于求解克服摩擦力做功问题,由于两段过程摩擦力大小不等,所以运用动能定理解决比较方便.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.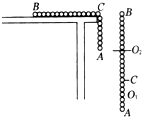 如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )
如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )
 如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )
如图所示,一长为L,质量为m的匀质柔软链条,放在光滑的水平桌面上,有$\frac{1}{3}$悬于桌外,求:放手后链条由静止开始运动至其左端刚要离开桌面的瞬间铁链条的速度是( )| A. | v=$\frac{1}{3}$gL | B. | $\frac{{\sqrt{3}}}{3}$gL | C. | $\sqrt{3}$gL | D. | v=$\frac{2}{3}\sqrt{2gL}$ |
6.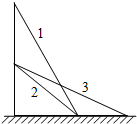 如图所示,有三个斜面1、2、3,斜面1与2底边相同,斜面2与3高度相同,同一物体与三个斜面间的动摩擦因数相同,当一物体分别沿三个斜面从顶端由静止下滑到底端时,下列说法正确的是( )
如图所示,有三个斜面1、2、3,斜面1与2底边相同,斜面2与3高度相同,同一物体与三个斜面间的动摩擦因数相同,当一物体分别沿三个斜面从顶端由静止下滑到底端时,下列说法正确的是( )
 如图所示,有三个斜面1、2、3,斜面1与2底边相同,斜面2与3高度相同,同一物体与三个斜面间的动摩擦因数相同,当一物体分别沿三个斜面从顶端由静止下滑到底端时,下列说法正确的是( )
如图所示,有三个斜面1、2、3,斜面1与2底边相同,斜面2与3高度相同,同一物体与三个斜面间的动摩擦因数相同,当一物体分别沿三个斜面从顶端由静止下滑到底端时,下列说法正确的是( )| A. | 下滑过程中物体损失的机械能△E3>△E2>△E1 | |
| B. | 下滑过程中因摩擦产生的热量Q1=Q2<Q3 | |
| C. | 到达底端时的速度v1>v2>v3 | |
| D. | 到达底端时的速度v1>v3>v2 |

 如图所示,一质量为M的小车用细线跨过一光滑定滑轮与一质量为m的物体相连,图中绳与水平方向的夹角为θ,整个系统处于静止状态,求:
如图所示,一质量为M的小车用细线跨过一光滑定滑轮与一质量为m的物体相连,图中绳与水平方向的夹角为θ,整个系统处于静止状态,求: 如图所示,质量均为m平板小车静止在光滑的水平面上,质量均为2m小孩以3m/s的初速度向右冲上小车,滑行一段后遇质量均为3m的障碍,小孩用力推障碍物,最后障碍物沿同一直线方向以3m/s的速度运动,且此过程中人和车没分开,求:
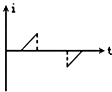
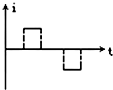
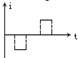
如图所示,质量均为m平板小车静止在光滑的水平面上,质量均为2m小孩以3m/s的初速度向右冲上小车,滑行一段后遇质量均为3m的障碍,小孩用力推障碍物,最后障碍物沿同一直线方向以3m/s的速度运动,且此过程中人和车没分开,求: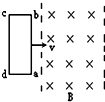 如图所示,一个由导体做成的矩形线圈,以恒定速率v运动,从无磁场区进入匀强磁场区,然后出来.若取逆时针方向为电流正方向,那么下图中的哪一个图线能正确地表示电路中电流与时间的函数( )
如图所示,一个由导体做成的矩形线圈,以恒定速率v运动,从无磁场区进入匀强磁场区,然后出来.若取逆时针方向为电流正方向,那么下图中的哪一个图线能正确地表示电路中电流与时间的函数( )