题目内容
9. 如图,固定在水平桌面上的“∠”型平行导轨足够长,间距L=1m,电阻不计.倾斜导轨的倾角θ=53°,并与R=2Ω的定值电阻相连.整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中.金属棒ab、cd的阻值为R1=R2=2Ω,cd棒质量m=1kg.ab与导轨间摩擦不计,cd与导轨间的动摩擦因数μ=0.3,设最大静摩擦力等于滑动摩擦力.现让ab棒从导轨上某处由静止释放,当它滑至某一位置时,cd棒恰好开始滑动.
如图,固定在水平桌面上的“∠”型平行导轨足够长,间距L=1m,电阻不计.倾斜导轨的倾角θ=53°,并与R=2Ω的定值电阻相连.整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中.金属棒ab、cd的阻值为R1=R2=2Ω,cd棒质量m=1kg.ab与导轨间摩擦不计,cd与导轨间的动摩擦因数μ=0.3,设最大静摩擦力等于滑动摩擦力.现让ab棒从导轨上某处由静止释放,当它滑至某一位置时,cd棒恰好开始滑动.(1)求此时通过ab棒的电流;
(2)求导体棒cd消耗的热功率与ab棒克服安培力做功的功率之比;
(3)若ab棒无论从多高的位置释放,cd棒都不动,则ab棒质量应小于多少?
(4)假如cd棒与导轨间的动摩擦因数可以改变,则当动摩擦因数满足什么条件时,无论ab棒质量多大、从多高位置释放,cd棒始终不动?
分析 (1)根据右手定则判断出ab棒产生的感应电流方向,确定出cd棒中感应电流方向,分析cd棒的受力情况,由平衡条件求解电流.
(2)根据题意画出等效电路如图所示:电阻R与cd棒并联,分析各部分电流关系,由功率公式求解即可.
(3)抓住ab棒匀速运动,cd棒都未滑动,分别对ab棒和cd棒分析,抓住cd棒安培力在水平方向上的分力小于最大静摩擦力,求出ab棒质量满足的条件.
(4)ab棒下滑时,cd棒始终静止,安培力的水平分力小于等于其最大静摩擦力,列出式子.当ab棒质量无限大,在无限长轨道上最终一定匀速运动,安培力FA趋于无穷大,cd棒所受安培力FAˊ亦趋于无穷大,讨论分析得解.
解答  解:(1)ab棒沿斜面滑下切割磁感线产生的感应电流的方向是b→a,通过cd棒的电流方向如图c→d.cd棒刚要开始滑动时,其受力分析如图所示.
解:(1)ab棒沿斜面滑下切割磁感线产生的感应电流的方向是b→a,通过cd棒的电流方向如图c→d.cd棒刚要开始滑动时,其受力分析如图所示.
由平衡条件得:BILcdcos53°=f
由摩擦力公式得:f=μN,N=mg+BILcdsin53°
联立以上三式,得:Icd=1.67A,Iab=2Icd=3.34A
(2)根据题意画出等效电路如图所示:
设Icd=I,因为电阻R与cd棒并联,故电阻R上产生的热功率与cd棒产生的热功率相等,即:${P_R}={P_{cd}}={I^2}R$
又因为流经ab棒的电流为2I,故ab棒产生的热功率为:${P_{ab}}=4{I^2}R$ 整个回路产生的热功率为:P=6I2R
整个回路产生的热功率为:P=6I2R
又因为回路中消耗的热功率源于ab棒克服安培力做功,所以导体棒cd消耗的热功率与ab棒克服安培力做功的功率之比为:
$\frac{Pcd}{PFA}$=$\frac{{{P_{cd}}}}{{{P_F}_A}}=\frac{{{I^2}R}}{{6{I^2}R}}=\frac{1}{6}$
(3)ab棒在足够长的轨道下滑时,最大安培力只能等于自身重力的分力,有:FA=mgabsin53°
cd棒所受最大安培力应为$\frac{1}{2}{F_A}$,要使cd棒不能滑动,需:$\frac{1}{2}{F}_{A}cos53°$≤μ(mg+$\frac{1}{2}{F}_{A}sin53°$)
由以上两式联立解得:mab≤2.08kg
(4)ab棒下滑时,cd棒始终静止,有:$\frac{1}{2}$FAcos53°≤μ(mg+$\frac{1}{2}$FAsin53°)
解得:μ≥$\frac{\frac{1}{2}{F}_{A}cos53°}{mg+\frac{1}{2}{F}_{A}sin53°}$=$\frac{cos53°}{\frac{mg}{{F}_{A}}+sin53°}$
当ab棒质量无限大,在无限长轨道上最终一定匀速运动,安培力FA趋于无穷大,cd棒所受安培力FAˊ亦趋于无穷大,有:μ≥$\frac{cos53°}{sin53°}$=0.75
答:(1)此时通过ab棒的电流为3.34A;
(2)导体棒cd消耗的热功率与ab棒克服安培力做功的功率之比为1:6;
(3)若ab棒无论从多高的位置释放,cd棒都不动,则ab棒质量应小于2.08kg.
(4)假如cd棒与导轨间的动摩擦因数可以改变,则当动摩擦因数满足μ≥0.75的条件时,无论ab棒质量多大、从多高位置释放,cd棒始终不动.
点评 本题是复杂的电磁感应现象,是电磁感应与力学知识、电路的综合,要能够正确地受力分析,抓住临界情况,结合共点力平衡和能量守恒进行求解.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案 某同学在操场上进行慢跑锻炼,并用智能手表记录了运动轨迹、运 动时间、运动距离和消耗热量的情况,如图,其中“S”是起点,“E”是终点,且根据操场实际情况可知,S和E间的距离约为40m.下列说法正确的是( )
某同学在操场上进行慢跑锻炼,并用智能手表记录了运动轨迹、运 动时间、运动距离和消耗热量的情况,如图,其中“S”是起点,“E”是终点,且根据操场实际情况可知,S和E间的距离约为40m.下列说法正确的是( )| A. | 在记录运动轨迹时,人不能看成质点 | |
| B. | S和E间的距离约为40m指人发生的位移大小 | |
| C. | 运动距离1.45km除以运动时间是平均速度大小 | |
| D. | 用40m除以运动时间是人经过E点的瞬时速度大小 |

| A. | F1的施力者是弹簧 | B. | F2的反作用力是F3 | ||
| C. | F3的施力者是地球 | D. | F4的反作用力是F1 |
 如图,在沿水平方向以加速度a=1m/s2匀加速行驶的车厢中,斜靠着与水平方向成α=37°角的气缸.一质量m=2kg、横截面积S=10cm2的光滑活塞,将一定质量的气体封闭在气缸内,并与气缸保持相对静止.已知大气压强为p0=1×105Pa.下列说法正确的是( )
如图,在沿水平方向以加速度a=1m/s2匀加速行驶的车厢中,斜靠着与水平方向成α=37°角的气缸.一质量m=2kg、横截面积S=10cm2的光滑活塞,将一定质量的气体封闭在气缸内,并与气缸保持相对静止.已知大气压强为p0=1×105Pa.下列说法正确的是( )| A. | 气缸对活塞的弹力为16N | B. | 气缸对活塞的弹力为17.2N | ||
| C. | 气缸内气体的压强为1.1×105Pa | D. | 气缸内气体的压强为2.8×105Pa |
| A. | T1<T2 | B. | m1<m2 | C. | q1<q2 | D. | 都无法确定 |
 如图所示,均匀U形管内盛有液体,左右液面相平,左管用活塞封闭了一定量的气体A,右管封闭气体B,开始A、B两部分气体压强均为p,气柱的长度均为l,现将活塞缓慢上提,提升的高度为d,则此过程中( )
如图所示,均匀U形管内盛有液体,左右液面相平,左管用活塞封闭了一定量的气体A,右管封闭气体B,开始A、B两部分气体压强均为p,气柱的长度均为l,现将活塞缓慢上提,提升的高度为d,则此过程中( )| A. | 气柱A的长度增加量等于d | B. | 气柱B的长度增加量小于d | ||
| C. | 气体A的最终压强小于$\frac{lp}{(l+d)}$ | D. | 气体A的最终压强大于$\frac{lp}{(l+d)}$ |
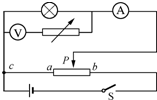 为了描绘小灯泡的伏安特性曲线,实验室可供选择的器材如下:
为了描绘小灯泡的伏安特性曲线,实验室可供选择的器材如下:
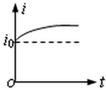
 水平方向的匀强磁场的上下边界分别是MN、PQ,磁场宽度为L.一个边长为a的正方形导线框(L>2a)从磁场上方下落,运动过程中上下两边始终与磁场边界平行,如图甲所示.线框进入磁场过程中感应电流i随时间t变化的图象如图乙,则线框从磁场中穿出过程中线框中感应电流i随时间t变化的图象可能是下图中的哪一个 ( )
水平方向的匀强磁场的上下边界分别是MN、PQ,磁场宽度为L.一个边长为a的正方形导线框(L>2a)从磁场上方下落,运动过程中上下两边始终与磁场边界平行,如图甲所示.线框进入磁场过程中感应电流i随时间t变化的图象如图乙,则线框从磁场中穿出过程中线框中感应电流i随时间t变化的图象可能是下图中的哪一个 ( )