��Ŀ����
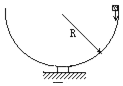
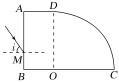
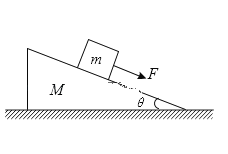
����Ŀ����ͼ��ʾ��AB��Ϊһ�뾶R��0.2 m�Ĺ⻬![]() Բ�������EF��һ���Ϊ30�����㹻���Ĺ⻬�̶�б�棬б������һ����Ϊ0.1 kg�ı�ľ��CD����ʼʱ��ľ�屻������һ����ҲΪ0.1 kg�����(ͼ��δ����)��A���ɾ�ֹ��ʼ�»���ͨ��B���ˮƽ�׳�������һ��ʱ���ǡ����ƽ���ڱ�ľ��ķ����ϱ�ľ�壬����黬�ϱ�ľ���ͬʱ��ľ�����������»�������ijʱ�����ͱ�ľ���ܴﵽ��ͬ�ٶȣ���֪����뱡ľ���Ķ�Ħ������Ϊ����
Բ�������EF��һ���Ϊ30�����㹻���Ĺ⻬�̶�б�棬б������һ����Ϊ0.1 kg�ı�ľ��CD����ʼʱ��ľ�屻������һ����ҲΪ0.1 kg�����(ͼ��δ����)��A���ɾ�ֹ��ʼ�»���ͨ��B���ˮƽ�׳�������һ��ʱ���ǡ����ƽ���ڱ�ľ��ķ����ϱ�ľ�壬����黬�ϱ�ľ���ͬʱ��ľ�����������»�������ijʱ�����ͱ�ľ���ܴﵽ��ͬ�ٶȣ���֪����뱡ľ���Ķ�Ħ������Ϊ����![]() .(g��10 m/s2������ɱ�������)��
.(g��10 m/s2������ɱ�������)��

(1)��鵽��B��ʱ��Բ�������ѹ����С��
(2)��黬�ϱ�ľ��ʱ���ٶȴ�С��
(3)�ﵽ��ͬ�ٶ�ǰ����»��ļ��ٶȴ�С������黬�ϱ�ľ�����ﵽ��ͬ�ٶ����õ�ʱ�䣮
���𰸡�(1)3 N��������ֱ���� (2)![]() m/s (3)
m/s (3)![]() s
s
��������
���� (1)����A��B�Ĺ��̣��ɶ��ܶ����ã�
mgR��![]() mv
mv![]() ��
��
��ã�vB��2 m/s ��
��B����ţ�ٵڶ����ɵã�
FN��mg��m![]() ��
��
��ã�FN��3 N ��
��ţ�ٵ������ɵ����Թ����ѹ����СΪ3 N��������ֱ������
(2)����黬�ϱ�ľ����ٶ�Ϊv���� cos 30����![]() ��
��
��ã�v��![]() m/s��
m/s��
(3)���ͱ�ľ���»������У���ţ�ٵڶ����ɵã�
����飺mgsin 30������mgcos 30����ma1 ��
�Ա�ľ�壺mgsin 30������mgcos 30����ma2 ��
�����ͱ�ľ��ﵽ�Ĺ�ͬ�ٶ�Ϊv������v����v��a1t��a2t ��
��ã�t��![]() s
s

 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�