Question

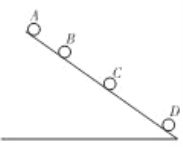
【题目】如图所示，从斜面上某一位置先后由静止释放四个小球.相邻两小球释放的时间间隔为0.1s，某时刻拍下小球所处位置的照片，测出SAB=6cm，SBC=12cm，SCD=18cm.则（ ）

A. 小球从A点释放

B. B点小球速度是A、D点小球速度之和的一半

C. C点小球的速度大小为1.5m/s

D. D点小球的加速度最大

Answer 1

【答案】C

【解析】

根据连续相等时间内的位移之差是一恒量求出小球的加速度，根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点小球的速度，结合速度时间公式求出A点小球的速度，从而判断是否从A点释放．根据平均速度推论分析C点小球和B、D两球速度的关系．

D、根据△x=aT2得，小球的加速度，则小球做加速度恒定的匀加速直线运动；故D错误.

B、根据匀变速直线运动的推论可知，B点的速度等于AC段的平均速度；故B错误.

C、C点是BD段的中间时刻，根据平均速度的推论知；故C正确.

A、A点小球的速度vA=vC-2aT=1.5-2×6×0.1m/s=0.3m/s≠0，可知小球不是从A点释放；故A错误.

故选C.