题目内容
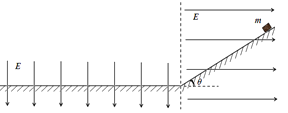
【题目】如图所示,倾角为30°的光滑斜面与粗糙的水平面平滑连接.现将一滑块(可视为质点)从斜面上A点由静止释放,最终停在水平面上的C点.已知A点距水平面的高度h=0.8 m,B点距C点的距离L=2.0 m(滑块经过B点时没有能量损失,g取10 m/s2),求:

(1)滑块在运动过程中的最大速度的大小;
(2)滑块与水平面间的动摩擦因数μ;
(3)滑块从A点释放后,经过时间t=1.0 s时速度的大小.
【答案】(1)4 m/s (2)0.4 (3)3.2 m/s
【解析】
试题分析:(1)滑块先在斜面上做匀加速运动,然后在水平面上做匀减速运动,设滑块在斜面上的加速度为a1,滑块运动到B点时速度大小为vm,则:mgsin30°=ma1
![]()
解得:vm=4m/s.
(2)设滑块在水平面上运动的加速度大小为a2,则:μmg=ma2
v![]() =2a2L,
=2a2L,
解得μ=0.4.
(3)滑块在斜面上运动的时间为t1,有vm=a1t1,
解得: ![]()
由于t>t1,故滑块已经经过B点,做匀减速运动的时间为t-t1=0.2 s
设t=1.0 s时速度大小为v,有v=vm-a2(t-t1)
解得:v=3.2 m/s.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目