题目内容
【题目】静止的镭核![]() 发生衰变,放出一个α粒子变为氡核Rn,已知镭核的质量为224.0248u,氡核的质量为220.0162u,α粒子的质量为4.0026u.(1u=931.5MeV的能量)
发生衰变,放出一个α粒子变为氡核Rn,已知镭核的质量为224.0248u,氡核的质量为220.0162u,α粒子的质量为4.0026u.(1u=931.5MeV的能量)
(1)写出核反应方程
(2)镭核衰变放出多少MeV的能量(结果保留2位有效数字)
(3)若衰变放出的能量全部转变为氡核和α粒子的动能,沿用第二问的结果,求出氡核的动能为多少MeV(结果保留1位有效数字)
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:根据电荷数守恒、质量数守恒写出衰变方程;根据爱因斯坦质能方程即可求出释放的能量;根据能量守恒定律以及动量守恒定律即可求出氡核的动能。
(1)根据电荷数守恒、质量数守恒得![]()
(2)质量亏损为:![]()
释放的核能为:![]()
(3)衰变过程中动量守恒,放出的能量全部转化为α粒子和氡核的动能
衰变过程根据动量守恒:![]()
能量关系为:![]()
解得氡核的动能为:![]()

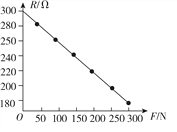
【题目】有一种测量压力的电子秤,其原理如图所示.E是内阻不计、电动势为6 V的电源.R0是一个阻值为300 Ω的限流电阻.G是由理想电流表改装成的指针式测力显示器.R是压敏电阻,其阻值可随压力大小的变化而改变,其关系如下表所示.C是一个用来保护显示器的电容器.秤台所受的重力忽略不计.(计算中用到的E一律代入6 V,R0一律代入300 Ω)
压力F/N | 0 | 50 | 100 | 150 | 200 | 250 | 300 | … |
电阻R/Ω | 300 | 280 | 260 | 240 | 220 | 200 | 180 | … |
(1)如图为描绘出的电阻R随压力F变化的一次函数,归纳出电值R随压力F变化的函数关系式_______
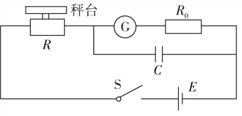
(2)台秤空载时,显示器指针在原电流表盘_____________A位置处.
(3)若电容器的耐压值为5 V,该电子秤的量程是____________ N
(4)写出压力F随电流I变化的关系式__________,说明该测力显示器的刻度________(均匀或不均匀)