题目内容
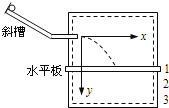
【题目】如图所示的阴极射线管,无偏转电场时,电子束加速后打到荧屏中央形成亮斑.如果只逐渐增大M1M2之间的电势差,则( )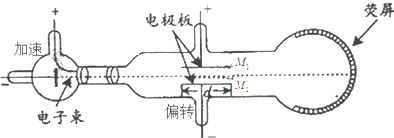
A.在荧屏上的亮斑向下移动
B.在荧屏上的亮斑向下移动
C.偏转电场对电子做的功增大
D.偏转电场的电场强度减小
【答案】C
【解析】A、B、设电子由加速电场加速后的速度为v . 电子在加速电场中运动过程,由动能定理得:
eU1= ![]()
解得,v= ![]() .
.
电子进入偏转电场后做匀变速曲线运动,沿极板方向做匀速直线运动,沿电场线方向做初速度为零的匀加速直线运动,则有:
水平方向有:L=vt
竖直方向有:a= ![]()
v=at
电子刚离开偏转电场时的偏转角正切为:tanα= ![]()
由以上各式解得:电子刚离开偏转电场时偏转角的正切为:tanα= ![]() ,
,
则α=arctan![]() .
.
即电子离开偏转电场时的偏转角α随偏转电压的增大而增大.如果只逐渐增大M1M2之间的电势差U2 , 在荧屏上的亮斑向上移动.故A不正确,B错误;
C、电子离开偏转电场时的偏转量:y= ![]() =
= ![]() ,
,
如果只逐渐增大M1M2之间的电势差U2 , 电子离开偏转电场时的偏转量将增大.
偏转电场对电子做的功:W=eEy , 偏转量越大,电场力做的功越多.故C正确;
D、偏转电场的电场强度:E= ![]() ,所以如果只逐渐增大M1M2之间的电势差U2 , 偏转电场的电场强度增大.故D错误.
,所以如果只逐渐增大M1M2之间的电势差U2 , 偏转电场的电场强度增大.故D错误.
故选:C
电子在加速电场中运动时,电场力做正功,电子获得速度,根据动能定理求解电子离开加速电场后的速度;
电子垂直进入偏转电场后做类平抛运动,平行于极板方向做匀速直线运动,垂直于极板方向做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学公式求得偏转量的表达式与电场力做功的表达式,即可进行说明.

 阅读快车系列答案
阅读快车系列答案【题目】弹簧自然悬挂,待弹簧竖直时,长度记为L自 , 弹簧下端挂上砝码盘时,长度记为L0;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6 , 数据如下表表:
|
(1)表中有一个数值记录不规范,代表符号为 . 由表可知所用刻度尺的最小分度为 .
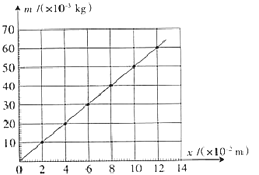
(2)图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与的差值(填“L自或L0”).
(3)由图可知弹簧和的劲度系数为N/m;通过图和表可知砝码盘的质量为g(结果保留两位有效数字,重力加速度取9.8m/s2).