题目内容
17.小球A从离地45m高处从静止开始自由下落,同时B球以初速度v0=20m/s从地面竖直向上抛出,A和B不在同一竖直线上运动,A和B落地后都不反弹,不计空气阻力,g取10m/s2,求:(1)从A开始下落到A和B在空中处于同一水平高度所需的时间;
(2)当A落地时,B离地高度和速度;
(3)若要使两球在B球下降过程中相遇(即处于同一水平高度),则v0应满足什么条件?
分析 (1)A球做竖直上抛运动,B球做自由落体运动,根据速度位移关系公式列式求解;
(2)先根据速度时间关系公式求解A球的运动时间,再根据位移时间关系公式求解B球的位移,结合几何关系判断离地高度.由速度时间公式求速度.
(3)先由相遇时位移大小之和等于45m求解时间t的表达式,再根据t满足的条件:$\frac{{v}_{0}}{g}$<t<$\frac{2{v}_{0}}{g}$,解答即可.
解答 解:(1)A球做竖直上抛运动,B球做自由落体运动,根据速度位移关系公式,有:
hA+hB=H
即:$\frac{1}{2}$gt2+(v0t-$\frac{1}{2}$gt2)=H
解得:t=$\frac{H}{{v}_{0}}$=$\frac{45}{20}$s=2.25s
(2)A落地时,根据位移时间关系公式,有:
H=$\frac{1}{2}g{t}_{A}^{2}$,
解得:tA=$\sqrt{\frac{2H}{g}}$=$\sqrt{\frac{2×45}{10}}$s=3s
此时B球的位移为:
x=v0tA-$\frac{1}{2}$gtA2=20×3-$\frac{1}{2}$×10×9=15m
即B球离地高度为15m;
速度为:v=v0-gtA=20-10×3=-10m/s,即方向竖直向下.
(3)若要使两球在B球下降过程中相遇,t必须满足:$\frac{{v}_{0}}{g}$<t<$\frac{2{v}_{0}}{g}$
又 t=$\frac{H}{{v}_{0}}$
联立解得:$\sqrt{\frac{1}{2}gH}$<v0<$\sqrt{gH}$
代入解得:15m/s<v0<15$\sqrt{2}$m/s.
答:(1)从A开始下落到A和B在空中处于同一水平高度所需的时间是2.25s;
(2)当A落地时,B离地高度是15m,速度大小为10m/s,方向竖直向下;
(3)若要使两球在B球下降过程中相遇(即处于同一水平高度),则v0应满足的条件是15m/s<v0<15$\sqrt{2}$m/s.
点评 本题关键是明确竖直上抛运动和自由落体运动的运动性质,然后根据运动学公式列式求解.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案| A. | 物体只有重心受到重力的作用 | |
| B. | 同一物体在不同纬度上所受的重力大小不同 | |
| C. | 在宇宙飞船中的物体处于完全失重状态,即不受重力的作用 | |
| D. | 重力的方向总是竖直向下 |
 沿同一条直线运动的a、b两个质点,在0~t0时间内的x-t图象如图所示,则下列说法正确的是( )
沿同一条直线运动的a、b两个质点,在0~t0时间内的x-t图象如图所示,则下列说法正确的是( )| A. | 质点a做周期性的往返运动 | |
| B. | t′时刻,a、b的位置不同 | |
| C. | 在0~t′时间内,a、b的位移和路程都相同 | |
| D. | 在0~t0时间内,a通过的路程是b通过路程的两倍 |
| A. | 质点的加速度大小为2m/s2 | B. | 质点从A点运动到C点历时3s | ||
| C. | 质点在C点的速度大小为llm/s | D. | 质点在B点的速度大小为6m/s |
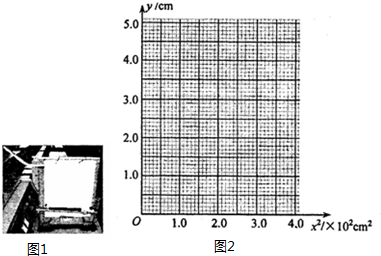 用如图1的装置做“研究平抛物体运动”的实验时,实验简要步骤如下:
用如图1的装置做“研究平抛物体运动”的实验时,实验简要步骤如下:①取下白纸,以O为原点,以竖直线为y轴、水平为x轴建立平面直角坐标系,用平滑曲线画出平抛轨迹;
②让小球多次从斜槽上同一位置由静止滚下,记下小球平抛运动中的一系列位置;
③安装好器材,调节斜槽,使斜槽的末端水平,记下小球离开斜槽时的位置O点和过O点的竖直线;
④测量曲线上某点的坐标x、y,算出小球的平抛初速度,实验需从曲线上取多个点求v0的值,然后求它们的平均值.
(1)上述步骤的合理顺序是③②④①(只排列序号).
(2)进行数据处理时,某同学在小球的运动轨迹上依次选取M1、M2、M3、M4四点,测出这些点的横、纵坐标值如下表:(表中的x2值是根据x值计算得出的)
| M1 | M2 | M3 | M4 | |
| x/(cm) | 5.00 | 10.00 | 15.00 | 20.00 |
| x2(cm)2 | 25.00 | 100.00 | 225.00 | 400.00 |
| y/(cm) | 0.31 | 1.25 | 2.81 | 5.00 |
①利用表中数据在坐标系中作出y-x2图象;
②由图象可知,y与x2的关系是y=$\frac{g}{2{v}_{0}^{2}}$x2,由此可判断小球做平抛运动的轨迹是倾斜直线;
③由图象可求得,小球抛出时初速度的大小为2.0m/s(取g=10m/s2,保留两位有效数字).