题目内容
4. 如图所示,两束不同单色光P和Q射向半圆形玻璃砖,在O点的入射角分别为45°和30°,它们的出射光线是从圆心O点沿OF方向,OF与界面的夹角为30°,半圆形玻璃砖的半径为R,求:
如图所示,两束不同单色光P和Q射向半圆形玻璃砖,在O点的入射角分别为45°和30°,它们的出射光线是从圆心O点沿OF方向,OF与界面的夹角为30°,半圆形玻璃砖的半径为R,求:①两束光穿过玻璃砖所用的时间差;
②将P光线绕O点旋转,使其刚好发生全反射,则其旋转的角度为多少?
分析 ①根据折射定律求出两束的折射率,由v=$\frac{c}{n}$求出光在玻璃砖的传播速度,即可求得时间差.
②将P光线绕O点旋转,使其刚好发生全反射,入射角等于临界角,根据sinC=$\frac{1}{n}$求临界角C,即可得到P旋转的角度.
解答 解:①根据折射定律n=$\frac{sini}{sinr}$得光束P的折射率为:nP=$\frac{sin60°}{sin45°}$=$\frac{\sqrt{6}}{2}$,光束Q的折射率为:nQ=$\frac{sin60°}{sin30°}$=$\sqrt{3}$.
光在玻璃砖的传播速度分别为:vP=$\frac{c}{{n}_{P}}$,vQ=$\frac{c}{{n}_{Q}}$
故两束光穿过玻璃砖所用的时间差为:△t=tQ-tP=$\frac{R}{{v}_{Q}}$-$\frac{R}{{v}_{P}}$
联立解得:△t=$\frac{R(2\sqrt{3}-\sqrt{6})}{2c}$
②将P光线绕O点旋转,使其刚好发生全反射,入射角等于临界角,根据sinC=$\frac{1}{n}$得:
C=arcsin$\frac{1}{{n}_{P}}$=arcsin$\frac{\sqrt{6}}{3}$
则P光旋转的角度为:C-45°=arcsin$\frac{\sqrt{6}}{3}$-45°.
答:①两束光穿过玻璃砖所用的时间差为$\frac{R(2\sqrt{3}-\sqrt{6})}{2c}$.
②将P光线绕O点旋转,使其刚好发生全反射,则其旋转的角度为arcsin$\frac{\sqrt{6}}{3}$-45°.
点评 解决本题的关键要掌握折射定律、全反射条件.对于涉及全反射的问题,要紧扣全反射产生的条件:一是光从光密介质射入光疏介质;二是入射角大于等于临界角.正确作出光路图是解题的关键,并能灵活运用几何知识求解.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 氢原子只有几个能级 | |
| B. | 氢原子发出的是平行光 | |
| C. | 氢原子有时发光,有时不发光 | |
| D. | 氢原子辐射的光子的能量是不连续的 |
| A. | 静止在粗糙斜面上的物体 | |
| B. | 沿光滑斜面自由下滑的物体 | |
| C. | 在水平面内做匀速圆周运动的物体 | |
| D. | 竖直上抛运动运动到最高点的一瞬间 |
 如图所示电路,电源电动势保持不变,内阻不可忽略,闭合开关S,缓慢向右移动滑动变阻器的滑片P,这一过程中( )
如图所示电路,电源电动势保持不变,内阻不可忽略,闭合开关S,缓慢向右移动滑动变阻器的滑片P,这一过程中( )| A. | 电路的总电阻增大 | B. | 电压表V的示数逐渐变小 | ||
| C. | 电流表A的示数逐渐变小 | D. | 电流表A1的示数逐渐变大 |
 如图所示,粗细均匀的绝缘棒组成一边长为L的正方形线框,线框上均匀地分布着正电荷,O是线框的中心,现在线框右侧中点A处取下足够短的带电量为q的一小段,将其沿OA连线向右移动$\frac{L}{2}$的距离到B点处,若线框的其它部分的带电量与电荷分布保持不变,则此时O点的电场强度大小为( )
如图所示,粗细均匀的绝缘棒组成一边长为L的正方形线框,线框上均匀地分布着正电荷,O是线框的中心,现在线框右侧中点A处取下足够短的带电量为q的一小段,将其沿OA连线向右移动$\frac{L}{2}$的距离到B点处,若线框的其它部分的带电量与电荷分布保持不变,则此时O点的电场强度大小为( )| A. | k$\frac{q}{{L}^{2}}$ | B. | k$\frac{3q}{2{L}^{2}}$ | C. | k$\frac{3q}{{L}^{2}}$ | D. | k$\frac{5q}{{L}^{2}}$ |
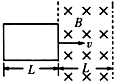 如图所示,矩形线框以恒定速度v自左向右通过有直线边界的匀强磁场,线框宽度等于磁场区域宽度,则在整个过程中,下列说法正确的是( )
如图所示,矩形线框以恒定速度v自左向右通过有直线边界的匀强磁场,线框宽度等于磁场区域宽度,则在整个过程中,下列说法正确的是( )| A. | 线框中的感应电流方向是先逆时针方向,后顺时针方向 | |
| B. | 线框中的感应电流方向是先顺时针方向,后逆时针方向 | |
| C. | 线框进入磁场过程中所受安培力方向向左 | |
| D. | 线框离开磁场过程中所受安培力方向向右 |
 如图所示,两个半径不同而内壁光滑的半圆轨道,固定于地面上,两个相同的小球从与球心同一水平高度上的A、B两点,由静止开始自由下滑,以A点为零势能参考平面,则两球通过轨道最低点时( )
如图所示,两个半径不同而内壁光滑的半圆轨道,固定于地面上,两个相同的小球从与球心同一水平高度上的A、B两点,由静止开始自由下滑,以A点为零势能参考平面,则两球通过轨道最低点时( )| A. | 小球对两轨道的压力不同 | B. | 小球对两轨道的压力相同 | ||
| C. | 小球的机械能不相等 | D. | 小球的机械能相等 |
| A. | 物体吸收热量,其温度一定升高 | |
| B. | 外界对气体做功,气体的内能一定增大 | |
| C. | 要使气体的分子平均动能增大,外界必须向气体传热 | |
| D. | 同种气体温度越高分子平均动能越大 |