题目内容
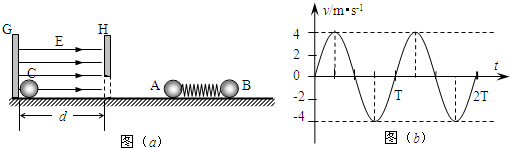
如图,光滑水平面上固定着一对竖直放置的平行金属板G和H.在金属板G右壁固定一个可视为质点的小球C,其质量为 MC=0.01kg、带电量为q=+1×10-5C.G、H两板间距离为d=10cm,板H下方开有能让小球C自由通过的小洞.质量分别为MA=0.01kg和MB=0.02kg的不带电绝缘小球A、B用一轻质弹簧连接,并用细线栓连使弹簧处于压缩状态,静放在H板右侧的光滑水平面上,如图(a)所示.现将细线烧断,小球A、B在弹簧作用下做来回往复运动(A球不会进入G、H两板间).以向右为速度的正方向,从烧断细线断开后的某时刻开始计时,得到A球的速度-时间图象如图(b)所示.
(1)求在t=0、
、
时刻小球B的速度,并在图(b)中大致画出B球的速度-时间图象;
(2)若G、H板间是电场强度为E=8×104V/m的匀强电场,在某时刻将小球C释放,则小球C离开电场时的速度为多大?若小球C以离开电场时的速度向右匀速运动,它将遇到小球A,并与之结合在一起运动,试求弹簧的最大弹性势能的范围.

(1)求在t=0、
| T |
| 4 |
| 3T |
| 4 |
(2)若G、H板间是电场强度为E=8×104V/m的匀强电场,在某时刻将小球C释放,则小球C离开电场时的速度为多大?若小球C以离开电场时的速度向右匀速运动,它将遇到小球A,并与之结合在一起运动,试求弹簧的最大弹性势能的范围.
分析:(1)对于小球A、B与轻质弹簧组成的系统,当烧断细线后动量守恒,根据A球的速度-时间图象得出B球的速度-时间图象
(2)当金属板间加有匀强电场时,电场力对小球做功,小球获得初动能并离开金属板,根据动能定理列出等式,水平方向A、B、C三小球系统不受外力,故系统动量守恒,当三球速度相同时弹簧的弹性势能最大,根据能量守恒求解.
(2)当金属板间加有匀强电场时,电场力对小球做功,小球获得初动能并离开金属板,根据动能定理列出等式,水平方向A、B、C三小球系统不受外力,故系统动量守恒,当三球速度相同时弹簧的弹性势能最大,根据能量守恒求解.
解答: 解:(1)对于小球A、B与轻质弹簧组成的系统,当烧断细线后动量守恒,有MAvA+MBvB=0
解:(1)对于小球A、B与轻质弹簧组成的系统,当烧断细线后动量守恒,有MAvA+MBvB=0
vB=-
=-
vA=-
vA
当t=0时,有 vB1=-
vA=-
×0=0
当t=
时,有 vB2=-
vA=-
×4m/s=-2m/s
当t=
时,有 vB3=-
vA=-
×(-4)m/s=2m/s
小球B的速度-时间图象如图所示.
(2)当金属板间加有匀强电场时,电场力对小球做功,小球获得初动能并离开金属板.
由动能定理,有 qEd=
MC
得 vC=
=4m/s
因水平方向A、B、C三小球系统不受外力,故系统动量守恒.
由此可得,不论A、C两球何时何处相碰,三球的共同速度是一个定值,
即三球速度相同时的总动能是一定值.
由MCvC=(MA+MB+MC)v共,
解得v共=1m/s
当三球速度相同时弹簧的弹性势能最大.
当A球在运动过程中速度为4m/s且与C球同向时,跟C球相碰,系统损失能量最小(为0),此情况下三球在运动过程中弹簧具有的最大弹性势能设为E1
E1=
+
+
-
(MA+MB+MC)
=0.18J
当A球在运动过程中速度为4m/s与C球反向时,跟C球相碰,系统损失能量最大,此情况下三球运动的过程中弹簧具有的最大弹性势能设为E2
由MCvC-MAvA=(MA+MC)v3,解得v3=0
E2=
(MA+MC)v32+
MBvB2-
(MA+MB+MC)v共2=0.02J
由上可得:弹簧具有的最大弹性势能的可能值在0.02J~0.18J的范围内.
答:(1)在t=0、
、
时刻小球B的速度分别是0,-2m/s,2m/s.
B球的速度-时间图象如图;
(2)弹簧的最大弹性势能的范围是0.02J~0.18J.
 解:(1)对于小球A、B与轻质弹簧组成的系统,当烧断细线后动量守恒,有MAvA+MBvB=0
解:(1)对于小球A、B与轻质弹簧组成的系统,当烧断细线后动量守恒,有MAvA+MBvB=0vB=-
| MAvA |
| MB |
| 0.01 |
| 0.02 |
| 1 |
| 2 |
当t=0时,有 vB1=-
| 1 |
| 2 |
| 1 |
| 2 |
当t=
| T |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
当t=
| 3T |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
小球B的速度-时间图象如图所示.
(2)当金属板间加有匀强电场时,电场力对小球做功,小球获得初动能并离开金属板.
由动能定理,有 qEd=
| 1 |
| 2 |
| v | 2 C |
得 vC=
|
因水平方向A、B、C三小球系统不受外力,故系统动量守恒.
由此可得,不论A、C两球何时何处相碰,三球的共同速度是一个定值,
即三球速度相同时的总动能是一定值.
由MCvC=(MA+MB+MC)v共,
解得v共=1m/s
当三球速度相同时弹簧的弹性势能最大.
当A球在运动过程中速度为4m/s且与C球同向时,跟C球相碰,系统损失能量最小(为0),此情况下三球在运动过程中弹簧具有的最大弹性势能设为E1
E1=
| 1 |
| 2 |
| MAv | 2 A |
| 1 |
| 2 |
| MBv | 2 B |
| 1 |
| 2 |
| MCv | 2 C |
| 1 |
| 2 |
| v | 2 共 |
当A球在运动过程中速度为4m/s与C球反向时,跟C球相碰,系统损失能量最大,此情况下三球运动的过程中弹簧具有的最大弹性势能设为E2
由MCvC-MAvA=(MA+MC)v3,解得v3=0
E2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由上可得:弹簧具有的最大弹性势能的可能值在0.02J~0.18J的范围内.
答:(1)在t=0、
| T |
| 4 |
| 3T |
| 4 |
B球的速度-时间图象如图;
(2)弹簧的最大弹性势能的范围是0.02J~0.18J.
点评:该题主要考查了系统动量守恒和能量守恒的应用,要分析物体的运动过程,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?郴州二模)如图所示,光滑水平面上有一小车B,右端固 定一砂箱,砂箱左侧连接一水平轻弹簧,小车和砂箱的总质量为M,车上放一小物体A,质量也是M,小物体A随小车以速度v0向右匀速运动,此时弹簧处于自由长度状态(小物体A与弹簧没有连接).小物体A与左侧车面间有摩擦,动摩擦因数为μ,与其它车面间无摩擦,在匀速运动时,距砂面H高处有一质量为m的泥球自由下落,恰好落在砂箱中.求:
(2013?郴州二模)如图所示,光滑水平面上有一小车B,右端固 定一砂箱,砂箱左侧连接一水平轻弹簧,小车和砂箱的总质量为M,车上放一小物体A,质量也是M,小物体A随小车以速度v0向右匀速运动,此时弹簧处于自由长度状态(小物体A与弹簧没有连接).小物体A与左侧车面间有摩擦,动摩擦因数为μ,与其它车面间无摩擦,在匀速运动时,距砂面H高处有一质量为m的泥球自由下落,恰好落在砂箱中.求: 如图所示,小车由光滑的弧形段AB和粗糙的水平段BC组成,静止在光滑水平面上,当小车固定时,从A点由静止滑下的物体到C点恰好停止.如果小车不固定,物体仍从A点静止滑下,则( )
如图所示,小车由光滑的弧形段AB和粗糙的水平段BC组成,静止在光滑水平面上,当小车固定时,从A点由静止滑下的物体到C点恰好停止.如果小车不固定,物体仍从A点静止滑下,则( )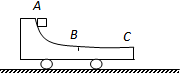 如图所示,小车由光滑的弧形段AB和粗糙的水平段BC组成,静止在光滑水平面上,当小车固定时,从A点由静止滑下的物体到C点恰好停止.如果小车不固定,物体仍从A点静止滑下,则( )
如图所示,小车由光滑的弧形段AB和粗糙的水平段BC组成,静止在光滑水平面上,当小车固定时,从A点由静止滑下的物体到C点恰好停止.如果小车不固定,物体仍从A点静止滑下,则( )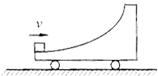 如图所示,一辆光滑曲面小车,静止在光滑水平面上,一木块以一定的速度开始沿小车曲面上滑,小车的质量为木块质量的4倍,当小车被固定时,木块沿曲面上滑的最大高度为h,求:
如图所示,一辆光滑曲面小车,静止在光滑水平面上,一木块以一定的速度开始沿小车曲面上滑,小车的质量为木块质量的4倍,当小车被固定时,木块沿曲面上滑的最大高度为h,求: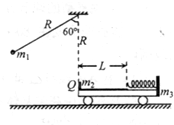 如图所示,静止在光滑水平面上的平板车,质量为m3=2kg,右端固定一自然伸长状态的轻弹簧,弹簧所在位置的车表面光滑,车左端和弹簧左端之间距离为L=0.75m,这部分车表面粗植,质量为m2=1kg的小物块Q,静止在平板车的左端.一不可伸长的轻质细绳长为R=2.5m,一端固定于Q正上方距Q为R处,另一端系一质量为m1=O.5kg的小球,将小球拉至悬线与竖直方向成60°角位置,由静止释放,小球到达最低点时与Q碰撞,时间极短,碰撞后小球反弹速度v0=lm/s,一段时间后Q恰好返回平板车左端静止.取g=10m/s2.求:
如图所示,静止在光滑水平面上的平板车,质量为m3=2kg,右端固定一自然伸长状态的轻弹簧,弹簧所在位置的车表面光滑,车左端和弹簧左端之间距离为L=0.75m,这部分车表面粗植,质量为m2=1kg的小物块Q,静止在平板车的左端.一不可伸长的轻质细绳长为R=2.5m,一端固定于Q正上方距Q为R处,另一端系一质量为m1=O.5kg的小球,将小球拉至悬线与竖直方向成60°角位置,由静止释放,小球到达最低点时与Q碰撞,时间极短,碰撞后小球反弹速度v0=lm/s,一段时间后Q恰好返回平板车左端静止.取g=10m/s2.求: