Question

【题目】如图所示，质量为m1=3kg的光滑圆弧形轨道ABC与一质量为m2=1kg 的物块P紧靠着（不粘连）静置于光滑水平面上，B为半圆轨道的最低点，AC为轨道的水平直径，轨道半径R=0.3m．一质量为m3=2kg的小球（可视为质点）从圆弧轨道的A处由静止释放，g取10m/s2，求：

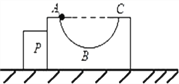
①小球第一次滑到B点时的速度v1；

②小球第一次经过B点后，相对B能上升的最大高度h．

Answer 1

【答案】(1)v1=2m/s,方向向右 (2)h=0.27m

【解析】试题分析：（i）设小球第一次滑到B点时的速度为v1，轨道和P的速度为v2，取水平向左为正方向，由水平方向动量守恒有（m1+m2）v2+m3v1=0

根据系统机械能守恒

联立解得v1="-2" m/s，方向向右；v2=1m/s，方向向左

（ii）小球经过B点后，物块P与轨道分离，小球与轨道水平方向动量守恒，且小球上升到最高点时与轨道共速，设为v，则有：m1v2+m3v1=（m1+m3）v

解得v=-0．2 m/s，方向向右

由机械能守恒

解得h=0．27 m