题目内容
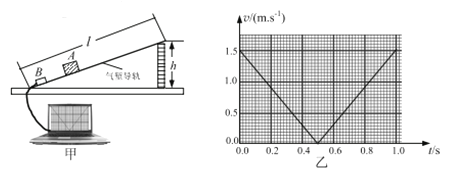
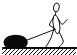
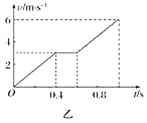
【题目】如图甲所示,两根质量均为0.1 kg完全相同的导体棒a、b,用绝缘轻杆相连置于由金属导轨PQ、MN架设的斜面上.已知斜面倾角θ为53°,a、b导体棒的间距是PQ、MN导轨的间距的一半,导轨间分界线OO′以下有方向垂直斜面向上的匀强磁场.当a、b导体棒沿导轨下滑时,其下滑速度v与时间的关系图象如图乙所示.若a、b导体棒接入电路的电阻均为1 Ω,其他电阻不计,取g=10 m/s2,sin 53°=0.8,cos 53°=0.6,试求:
(1)PQ、MN导轨的间距d;
(2)a、b导体棒与导轨间的动摩擦因数;
(3)匀强磁场的磁感应强度B的大小.
【答案】(1)1.2m(2)0.083(3)0.83T
【解析】(1)由图乙可知导体棒b刚进入磁场时a、b和轻杆所组成的系统做匀速运动,当导体棒a进入磁场后才再次做加速运动,因而b棒匀速运动的位移即为a、b棒的间距,依题意可得:
d=2vt=2×3×(0.6-0.4)m=1.2 m
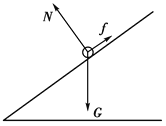
(2)设进入磁场前导体棒运动的加速度为a,由图乙得:
a=![]() =7.5 m/s2,因a、b一起运动,故可看作一个整体,其受力分析如图所示.由牛顿第二定律得:
=7.5 m/s2,因a、b一起运动,故可看作一个整体,其受力分析如图所示.由牛顿第二定律得:
2mgsin θ-μ2mgcos θ=2ma
解得:μ=(gsin θ-a)/(gcos θ)=(10×0.8-7.5)/(10×0.6)=0.5/6=0.083
(3)当b导体棒在磁场中做匀速运动时,有:
2mgsin θ-μ2mgcos θ-BId=0
I=![]()
联立解得:B=0.83 T

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目