Question

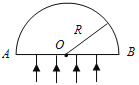
【题目】如图所示，圆管构成的半圆形竖直轨道固定在水平地面上，轨道半径为R，MN为直径且与水平面垂直，直径略小于圆管内径的小球A以某一初速度冲进轨道，到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞，碰后两球粘在一起飞出轨道，碰撞后两球的速度变为碰撞前的一半，落地点距N为2R．重力加速度为g，忽略圆管内径，空气阻力及各处摩擦均不计，求：

（1）粘合后的两球从飞出轨道到落地的时间t；

（2）小球A冲进轨道时在N点的速度大小．

Answer 1

【答案】（1）粘合后的两球从飞出轨道到落地的时间t为 ．（2）小球A冲进轨道时在N点的速度大小为 ．

【解析】本题考查动量守恒、平抛运动、机械能守恒等知识。

（1）粘合后的两球飞出轨道后做平抛运动，竖直方向分运动为自由落体运动，

有 …①

解得： …②

（2）设球A的质量为m，在N点速度为v，与小球B碰撞前速度大小为v1，把球A冲进轨道最低点时的重力势能定为0，由机械能守恒定律知 …③

设碰撞后粘合在一起的两球速度大小为v2，则

由动量守恒定律知 …④

综合②③④式得：